Практическое занятие №1
МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ Задача 1. Эксперимент говорит о том, что при взаимодействии веществ, находящихся в газообразном состоянии, выполняется закон кратных отношений объемов исходных веществ и продуктов реакции. Так, один объем водорода, соединяясь с одним объемом хлора, дает два объема хлористого водорода (объемы измеряются при одних и тех же температуре и давлении), два объема водорода, соединяясь с одним объемом кислорода, дают два объема водяного пара. Решение. а) Молекула хлористого водорода состоит из одного атома водорода и одного атома хлора. При соединении водорода и хлора хлористый водород получится без остатка только в том случае, если исходные вещества имели по одинаковому числу атомов водорода и атомов хлора. Отсюда можно сделать вывод, что в равных объемах водорода и хлора содержится равное число атомов. А так как в молекулах водорода и хлора содержится по одинаковому числу атомов, то из сформулированного выше вывода следует, что при одинаковых давлениях и температурах в равных объемах газов содержится одинаковое число молекул. Здесь следует обратить внимание на то, что данное утверждение и есть закон Авогадро [заметка об Амадео Авогадро и его законе имеется в журнале “Квант". N 12. 1986 г. С.12, 20]. б) При одинаковых давлениях и температурах в единицах объема содержится одно и то же число молекул, то есть одинаковы концентрации молекул: n1 и n2. Масса единицы объема газа (плотность r) - Вопрос об измерении числа Авогадро пока не обсуждается. Достаточно сообщить, что одни из первых опытов по измерению числа Авогадро провел Жан Перрен при изучении распределения плотности броуновских частиц в жидкости, находящейся в поле тяжести. Пока важно само число, а не способ измерения. Задача 2. Проводят реакцию образования окиси азота из азота и кислорода. Что получится в результате соединения 2 л азота с 1 л кислорода? Какой объем займет оставшийся газ после окончания реакции? Решение. После использования кислорода останется 1 литр неиспользованного азота, значит, после окончания реакции останется смесь азота и окиси азота. Так как из двух объемов кислорода и азота получается два объема окиси азота, оставшийся после реакции при поддержании постоянного давления газ займет: один литр азота и два литра окиси азота. Задача 3. Плотность жидкого азота при атмосферном давлении составляет rж=804 кг/м3, а плотность газообразного азота при том же давлении и температуре, равной 0оС, равна rж=1,25 кг/м3. Во сколько раз среднее расстояние между молекулами в газе превышает расстояние между молекулами в жидком состоянии? Решение. Разобьем объемы газа и жидкости на кубики такого объема b3, чтобы среднее число молекул, приходящихся на него, равнялось единице. Для вещества, находящегося в каком угодно состоянии (твердом, жидком, газообразном) можно считать, что b равно среднему расстоянию между центрами молекул. Тогда Задача 4. С помощью ионного проектора получена картина распределения атомов платины на острие. С помощью фрагмента фотографии экрана проектора на рисунке 3 оцените расстояния между атомами, если радиус кривизны острия иглы равен 96 нм, а радиус экрана 36 см, размер фрагмента 1 см. Решение помогает яснее представить себе работу ионного проектора. Из геометрических соображений очевидно, что увеличение ионного проектора равно отношению радиусов кривизны экрана и острия иглы. Согласно условию задачи, увеличение данного проектора равно Вопрос 1. Почему для демонстрации сил межмолекулярного взаимодействия используют свинцовые цилиндры, а не стальные? Ответ. Поверхность стального цилиндра, как бы тщательно не была обработана, является шероховатой. При соприкосновении двух поверхностей в непосредственном контакте находится небольшое число атомов. Соответственно, суммарная сила притяжения атомов, принадлежащих разным цилиндрам, оказывается малой, так что ее трудно заметить. Свинец является мягким металлом. При соприкосновении свинцовых цилиндров и одновременном относительном вращении шероховатости слипаются, что увеличивает число контактирующих атомов и суммарную силу притяжения. [Слипанию атомов препятствует также молекулярный слой из атмосферы и различных загрязнений. При разработке систем космических станций всерьез обсуждалась проблема возможного молекулярного прилипания деталей при случайном контакте]. Вопрос 2. Чем отличаются взаимодействия молекул воды во льде и в водяном паре? Ответ. Закон взаимодействия двух молекул воды от расстояния один и тот же, в каком бы состоянии не находилась вода с этими молекулами. Однако в газообразном состоянии большее время молекулы находятся на большом расстоянии друг от друга, поэтому большую часть времени сила взаимодействия мала и является притяжением. В состоянии льда молекулы колеблются около равновесного положения. Примерно одно и то же время молекулы отталкиваются и притягиваются друг к другу. При этом мгновенные значения силы взаимодействия гораздо больше, чем в газообразном состоянии. Таким образом, можно сказать, что взаимодействие между молекулами воды во льде сильнее, чем в газе и, что среднее значение силы взаимодействия равно нулю. Задача 5. График зависимости силы взаимодействия двух молекул от расстояния между ними имеет вид, показанный на рисунке 6. Для большого числа веществ его приближенно можно выразить формулой Решение позволяет более основательно повторить график зависимости силы взаимодействия между двумя молекулами. Предварительно полезно установить, какая часть графика описывает отталкивание молекул, а какая – притяжение. а) Вопрос на уточнение смысла равновесного расстояния между молекулами и точки пересечения графиком F(r) оси абсцисс. Так как это одно и то же, то опытными данными для определения b являются данные о плотности данного вещества в твердом состоянии. б) Растяжение вещества, находящегося в твердом состоянии, увеличивает расстояние между молекулами. Становится r>b. При этом твердое тело препятствует растяжению, что говорит о взаимном притяжении молекул. Другим фактом является конденсация газа в жидкость. В газообразном состоянии среднее расстояние между молекулами значительно больше, чем b. Слипание молекул и переход вещества в жидкое состояние указывает на наличие взаимного притяжения между молекулами. При сжатии жидкостей и твердых тел приходится создавать очень большие давления, чтобы достичь заметного уменьшения объема. Это говорит о возникновении отталкивания между молекулами при r<b. в) В выражении силы парного взаимодействия г) Дополнительный вопрос. Для его решения надо воспользоваться условием F(r0)=0. Из данного условия получаем: Задача 6. В селекторе скоростей диски расположены на расстоянии 1 м и вращаются со скоростью 3600 об/мин. Щели на дисках установлены под углом 45%. Какую скорость имели молекулы, пролетевшие через селектор скоростей? Решение. Скорость молекул, пролетевших через селектор скоростей при данных задачи, равна Вопрос 3. З ависит ли величина смещения изображения щели на внутренней стороне цилиндра от расстояния между цилиндром и печью? Ответ. Смещение изображения щели определяется временем пролета молекул внутри цилиндра и угловой скоростью цилиндра. Ни та, ни другая величина не зависят от расстояния между цилиндром и печью, поэтому ответ отрицательный - нет. Вопрос 4. Провели два эксперимента при двух значениях угловой скорости цилиндра w1 и w2, причем w1<w2, при прочих равных условиях; в каком случае смещение изображения щели оказалось большим? Ответ. В одних и тех же условиях средняя скорость молекул одна и та же, значит, одно и то же время пролета молекул внутри цилиндра; цилиндр, вращающийся с большей угловой скоростью, в заданное время успеет повернуться на больший угол, поэтому при w=w2 смещение изображения щели будет большим. Задача 7. Скорость молекул измерили с помощью установки с вращающимся цилиндром. Получите формулу, выражающую скорость молекулы v, попавшей в цилиндр, через угловую скорость, диаметр цилиндра D, и смещение изображения щели. Задача 8 [C5.1.10]. Оцените, во сколько раз поток газа, вытекающего из сосуда через цилиндрический канал радиуса R и длины L, меньше потока газа, вытекающего через отверстие радиуса R в бесконечно тонкой стенке. Считать, что стенки канала поглощают молекулы. Задача 9. На диск радиуса R равномерно рассыпан мак. Всего N семян. Координаты каждой семянки - случайные величины. Решение данной задачи преследует прежде всего цель освоиться, привыкнуть к понятию "плотность распределения". а) Из условия равномерности распределения семян следует, что число их на единицу площади одно и то же. Оно равно
Задача 10 [ C5.2.3 ]. Число молекул однородного идеального газа DN, скорость которых вдоль оси ОХ лежит в интервале ( ux; ux+Duk ), при данной температуре Т определяется выражением (N - полное число молекул) Решение. Использование рисунка можно провести в двух вариантах: 1) Значение плотности распределения молекул по проекциям скорости определяется измерением линейной ординаты графика f( v x) в точке v x=500 м/с и домножением на соответствующий множитель. 2) С помощью графика определяется предэкспоненциальный множитель а) Непосредственное измерение линейкой f( v x) в точке v x=500 м/с дает f(500)»2,5×10-4×N»2,5×10-4×2×1019=5×1015. Соответствующее число молекул DN= f( v x)D v x=5×1015×2=1016шт. б) В новой ситуации изменилось число N. Оно в 106 раз больше. Кроме того, длина интервала скоростей теперь в два раза больше и равна Р а с ч е т н а я м е т о д и к а: а) б) Ответ на этот вопрос в 2×106 раз больше, поэтому DN=2,4×1022 шт.
|


 . (2)
. (2)  (3)
(3)  . С помощью линеек на рисунке можно измерить число светящихся точек, укладывающихся на одном сантиметре. Измерения проводятся во внутреннем кольце. В зависимости от расположения атома относительно поверхности иглы получается более или менее яркая точка, поэтому на фотографии в промежутках между кольцами и во внешних кольцах не все атомы видны. Плотный ряд атомов дает только внутреннее кольцо. Подсчет можно проводить произвольно, так как получаемый результат является оценочным. Например так: измерить диаметр кольца D, а с ним и длину, а потом подсчитать число точек в кольце, тогда
. С помощью линеек на рисунке можно измерить число светящихся точек, укладывающихся на одном сантиметре. Измерения проводятся во внутреннем кольце. В зависимости от расположения атома относительно поверхности иглы получается более или менее яркая точка, поэтому на фотографии в промежутках между кольцами и во внешних кольцах не все атомы видны. Плотный ряд атомов дает только внутреннее кольцо. Подсчет можно проводить произвольно, так как получаемый результат является оценочным. Например так: измерить диаметр кольца D, а с ним и длину, а потом подсчитать число точек в кольце, тогда  , где n – число светящихся точек, приходящихся на 1 см, N - число светящихся точек во внутреннем кольце. Получается около 11 см-1. Таким образом, расстояние между атомами на поверхности иглы
, где n – число светящихся точек, приходящихся на 1 см, N - число светящихся точек во внутреннем кольце. Получается около 11 см-1. Таким образом, расстояние между атомами на поверхности иглы  .
.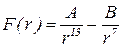 . Он пересекает ось абсцисс в одной точке r=b.
. Он пересекает ось абсцисс в одной точке r=b.  ,
, 
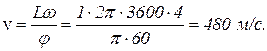


 б) Разобьем всю площадь диска на тонкие площадки равной удаленности от центра диска, то есть на кольца толщинами Dr1, Dr2Dr3,... Drk,...Drn. Все семянки, попавшие в кольца радиуса rk обладают свойством: они находятся в интервале расстояний до центра диска ( rk; rk+Drk ). Определим число семянок, попадающих в этот интервал
б) Разобьем всю площадь диска на тонкие площадки равной удаленности от центра диска, то есть на кольца толщинами Dr1, Dr2Dr3,... Drk,...Drn. Все семянки, попавшие в кольца радиуса rk обладают свойством: они находятся в интервале расстояний до центра диска ( rk; rk+Drk ). Определим число семянок, попадающих в этот интервал 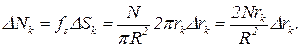

 , (4)
, (4)  , из него
, из него  , а затем значение f(500) определяется подстановкой найденных значений предэкспоненты и v 0 в формулу f( v x).
, а затем значение f(500) определяется подстановкой найденных значений предэкспоненты и v 0 в формулу f( v x). , отсюда
, отсюда  . Таким образом,
. Таким образом, 



