Распределение молекул по скоростям
3.2.1 Функция распределения. Функции распределения используют в тех ситуациях, когда имеют дело с большим числом случайных событий. С функцией распределения ознакомитесь на примере распределения ожидающих электричку пассажиров на платформе. Проведем ось ОХ вдоль платформы. Разобьем платформу на участки длинами Dx1, Dx2,... Dxk,... Dxm. Обозначим числа пассажиров, стоящих в ожидании электрички на каждом из участков DN1, DN2,... DNk,... DNm. Если для каждого из участков величина
Близким по смыслу распределением является распределение малых частиц по ящикам, имеющим разные координаты (доска Гальтона). В вертикальной доске забиты несколько горизонтальных рядов гвоздиков. Сверху на ряды высыпают частички - семена или мелкие камешки, или маленькие шарики. Каждая частичка после нескольких ударов о гвоздики отклоняется на некоторое расстояние по горизонтали и попадает в узкий ящик. Случайным событием является проход одной частицы по хаотической траектории. Результат проведения большого числа экспериментов описывается распределением частиц по ящикам - т.е. распределением частиц по координатам. В статистике чаще всего используют не распределение чисел событий, которое зависит от числа испытаний, а распределение относительных чисел - Рассмотрим еще один пример распределения событий. Посетитель магазина делает покупку на S рублей. Это случайное событие, сумма S - случайная величина. Если по оси абсцисс откладывать стоимость покупок одного посетителя, то аналогично распределению пассажиров по координатам можно построить распределение посетителей по суммам покупок. Разобьем ось стоимостей на отрезки DSi. Если DNi - число покупателей, сделавших покупки на суммы, лежащие в интервалах (Si; Si+DSi) и т.д., то величины 3.2.2 Молекулы газа в сосуде имеют разные скорости. [В результате столкновений скорости изменяются. Однако ясно, что если к газу энергия не подводится (и не отводится), то сумма кинетических энергий молекул со временем не изменяется]. Описать распределение молекул газа по скоростям можно аналогично рассмотренным выше примерам. Пусть v xi - случайные значения проекций скорости молекулы в какой-либо момент времени. Будем откладывать вдоль оси абсцисс возможные значения х-
Проведем аналогичные выше рассмотренным примерам рассуждения и введем плотность распределения f( v x) молекул по скоростям. Разобьем ось возможных значений х- проекции скорости молекулы на отрезки D v x. Обозначим числа молекул, попадающих в эти отрезки, через DNi, то есть DNi - число молекул, Распределение молекул по значениям скорости можно получить экспериментально. Для этого надо воспользоваться установкой Штерна с вращающимися щелью и улавливающим экраном в виде цилиндра. Если разбить размытое изображение щели цилиндра на улавливающем экране на тонкие полоски, то, очевидно, что число молекул, попавших в полоску, сдвинутую на расстояние S, равно числу молекул, скорость которых заключена в пределах от 4pR2w/S до 4pR2w/S/(S+DS), где R - радиус цилиндра, w - угловая скорость его вращения, DS - ширина выделенной полоски на изображении щели, созданном осевшими на внутренней поверхности цилиндра молекулами. Здесь важен сам принцип получения информации о распределении. Толщина слоя осевших молекул в данном месте пропорциональна числу попавших сюда частиц. Из измерений толщин полосок можно получать значения f( v x). Эксперимент, и теоретический анализ показывают, что Обсудим следующие свойства функции f( v x): - наибольшее значение функция принимает при наименьшем значении абсолютной величины показателя степени, значит, данная функция имеет максимум при v x=0; Эксперименты показали, что распределения молекул по каждой из проекций скоростей описываются одной и той же функцией (9).Постоянная С определяется из условия равенства интеграла от f( v x) единице: Используя тот факт, что распределение молекул по значениям проекций скоростей v x,v y и v z описываются одной и той же функцией, можно найти распределение молекул по абсолютному значению скорости. В интервал значений х -проекции скорости (v x; v x +dv x) попадает всего dN( v x)=Nf( v x)d v x молекул. Причем эти молекулы могут иметь какие угодно значения y- и z- проекций скорости. Из них только доля, равная f( v y)d v y, имеет y- проекцию скорости в интервале (v y; v y +dv y). Значит, число молекул, y- и z- проекции скорости которых заключены в соответствующих интервалах, равно Для нахождения распределения молекул по значениям модуля скорости построим трехмерную систему координат, на координатных осях которой будем откладывать значения проекций скоростей молекул v x,v y и v z (это воображаемое пространство скоростей). Молекула со скоростью, проекции которой, например, равны v x=120 м/с, v y=210 м/с, v z=90 м/с, в этой системе координат изобразится точкой. Каждая из молекул газа даст свою точку в данной системе координат. Плотность распределения молекул по проекциям скоростей - это плотность (густота) точек в данной системе координат. Плотность точек, согласно формуле (11), на расстоянии (i) от начала координат во всех направлениях одинакова. Если разбить пространство скоростей на сферические слои, то все точки, попавшие в один слой, будут изображать молекулы с одним и тем же модулем скорости При построении графика зависимости f( v ) будем иметь следующее. Множитель C3 задает вертикальный масштаб. При v<<v 0 показатель степени экспоненты близок к нулю, значит, сама экспонента мало отличается от единицы. Тогда f( v )»4pC3 v 2. Следовательно, при малых, по сравнению с v 0 скоростях, плотность распределения квадратично растет от нуля. Это говорит о том, что близкие к нулю значения скоростей молекул редко встречаются. При v<<v 0 ход зависимости f( v ) определяется быстро убывающей экспонентой и стремится к нулю. Таким образом, график f( v ) имеет максимум. Он приходится на значение модуля скорости v = v 0 Распределения молекул по проекциям скоростей и по модулю скорости определяются температурой и родом молекул, но не зависят от агрегатного состояния вещества, то есть одни и те же для газа, для жидкости и для твердого тела, если для всех состояний температура одна и та же. [Замечательно, что, несмотря на наличие сильного взаимодействия между молекулами в жидкостях и газах, где невозможно выделить промежутки времени прямолинейного полета, распределение молекул по скоростям при заданной температуре совпадает с распределением в газе.]
|

 одна и та же, то распределение пассажиров на платформе является равномерным. При малых значениях Dxk величину nk называют плотностью распределения координаты пассажиров. По прибытии электрички, до открытия дверей пассажиры группируются напротив них; образуются "сгустки". Теперь распределение не является равномерным. Величина nk теперь зависит от координаты участка. Произошло изменение распределения. Плотность распределения обладает очевидным свойством
одна и та же, то распределение пассажиров на платформе является равномерным. При малых значениях Dxk величину nk называют плотностью распределения координаты пассажиров. По прибытии электрички, до открытия дверей пассажиры группируются напротив них; образуются "сгустки". Теперь распределение не является равномерным. Величина nk теперь зависит от координаты участка. Произошло изменение распределения. Плотность распределения обладает очевидным свойством  , где N - полное число пассажиров на платформе. Размерность плотности распределения м-1. В приведенном примере случайным событием, или случайным экспериментом, является размещение пассажира в данном месте с координатой х. Координата х - случайная величина.
, где N - полное число пассажиров на платформе. Размерность плотности распределения м-1. В приведенном примере случайным событием, или случайным экспериментом, является размещение пассажира в данном месте с координатой х. Координата х - случайная величина. Рис. 8
Рис. 8
 . Если многократно проводить рассыпание частиц и в каждом эксперименте определять отношение, то среднее значение отношения
. Если многократно проводить рассыпание частиц и в каждом эксперименте определять отношение, то среднее значение отношения  будут описывать распределение посетителей по суммам покупок. ni – плотность распределения. В данной ситуации ее размерность равна руб-1. График, изображенный на рисунке, говорит, что существует наиболее часто встречающаяся сумма расходов посетителя Smax и что часть посетителей вообще не делают никаких покупок, и что ни один посетитель не израсходовал в магазине сумму большую maxS рублей.
будут описывать распределение посетителей по суммам покупок. ni – плотность распределения. В данной ситуации ее размерность равна руб-1. График, изображенный на рисунке, говорит, что существует наиболее часто встречающаяся сумма расходов посетителя Smax и что часть посетителей вообще не делают никаких покупок, и что ни один посетитель не израсходовал в магазине сумму большую maxS рублей.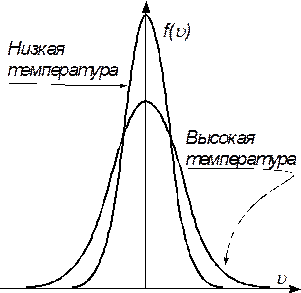 проекции скорости одной молекулы v x.
проекции скорости одной молекулы v x. . (8)
. (8)  (9)
(9) (10)
(10)  Это - трехмерная функция распределения молекул по проекциям скоростей.
Это - трехмерная функция распределения молекул по проекциям скоростей. (но различными проекциями v x,v y и v z скорости). Число точек, попадающих в такой слой, равно плотности распределения, умноженной на "объем" этого слоя. Он равен 4p v 2d v (4p v 2 - "площадь" слоя, d v - "толщина" слоя). Таким образом, число точек, попадающих в шаровой слой пространства скоростей, равное числу молекул, модуль скорости которых лежит в интервале от v до v + d v, определится формулой:
(но различными проекциями v x,v y и v z скорости). Число точек, попадающих в такой слой, равно плотности распределения, умноженной на "объем" этого слоя. Он равен 4p v 2d v (4p v 2 - "площадь" слоя, d v - "толщина" слоя). Таким образом, число точек, попадающих в шаровой слой пространства скоростей, равное числу молекул, модуль скорости которых лежит в интервале от v до v + d v, определится формулой:  (11)
(11)  (12)
(12)  . Это наиболее часто встречающееся значение модуля скорости. Быстрый спад f( v ) при v>>v 0 говорит о том, что большие, по сравнению с v 0, скорости у молекул редко встречаются.
. Это наиболее часто встречающееся значение модуля скорости. Быстрый спад f( v ) при v>>v 0 говорит о том, что большие, по сравнению с v 0, скорости у молекул редко встречаются.


