Энергетическая шкала температур
2.2.1 Рассмотрим столкновение двух молекул, имеющих массы m1 и m2. Обозначим скорость молекул до столкновения Изменение кинетической энергии первой частицы в результате столкновения равно минус изменению кинетической энергии второй частицы. Также равны изменения импульсов частиц:
где Разумеется, молекула находится в непрерывном беспорядочном процессе передачи и получения энергии от других молекул. 2.2.2 Пусть рассмотренные выше две молекулы находятсясреди других молекул в газе, находящемся в состоянии теплового равновесия. В состоянии теплового равновесия энергия любой молекулы в среднем постоянна, то есть, в частности, 2.2.3 Из рассмотрения обмена энергией между молекулами газа, находящегося в тепловом равновесии видно, что средняя кинетическая энергия молекул обладает первым свойством температуры: “Если две части системы имеют одинаковые средние кинетические энергии, то передача энергии между этими частями отсутствует”. Можно показать, что средняя кинетическая энергия молекул обладает и вторым свойством температуры. Для этого рассмотрим сосуд, разделенный на две части теплоизолирующей перегородкой. В одном отсеке находится газ, молекулы которого имеют среднюю кинетическую энергию á e1 ñ, в другом - á e2 ñ (при одном и том же давлении). Пока перегородка на месте, газ в обоих отсеках находится в тепловом равновесии. Каждая молекула одинаково часто отдает и принимает энергию при соударениях с другими молекулами. Допустим, á e1 ñ >;á e2 ñ. Если перегородку убрать, то, помимо соударений молекул с одинаковыми средними кинетическими энергиями, будут иметь место соударения молекул с разными средними кинетическими энергиями. При соударениях этого типа молекулы со средней энергией á e1 ñ чаще отдают, чем получают энергию. Имеет место передача энергии от части с большей средней кинетической энергией к части с меньшей средней кинетической энергией. Отсюда следует, что средняя кинетическая энергия молекул обладает и вторым свойством температуры. Таким образом, средняя кинетическая энергия может служить термометрическим параметром, причем этот параметр не зависит от рода термометрического вещества и в этом смысле является универсальным. Шкала, в которой температура измеряется в джоулях, называется универсальной (или энергетической) шкалой температур. Температура Т в исторически выбранных единицах, измеряемая в кельвинах, и температура в энергетической шкале, если газ является одноатомным, связаны соотношением Проведенный выше анализ не налагает на участвующие в теплообмене частицы никаких ограничений. Это могут быть и молекулы с сильно отличающимися массами и макроскопические (броуновские) частицы. Поскольку средние кинетические энергии молекул в состоянии теплового равновесия одинаковы, легкие частицы движутся быстрее, чем тяжелые. Из уравнения (28) следует: Рассмотрим пример. Задача. Сосуд разделен перегородкой на две части. Перегородка пористая и содержит огромное число тонких щелей. Газ, проникающий через щели, откачивается и собирается в специальную камеру. Левая часть сосуда заполняется разреженным газом из молекул с массами m1 и m2. Обозначим через c1 и c2 относительные концентрации молекул первого и второго типов соответственно. Эти концентрации поддерживаются постоянными в левой части сосуда из-за притока свежего газа в количестве, необходимом для компенсации утечки. Решение. Проведем расчет числа молекул, попадающих в отверстия перегородки за время Dt. Рассмотрим процесс пролета газа через отверстия, размеры которых много меньше длины свободного пробега молекул. Эта ситуация интересна следующими факторами: выход молекул из сосуда не изменяет распределения их по скоростям, в отверстии скорости молекул такие же, как и в сосуде, в отличие от того, что получается при выходе газа через большое отверстие. В первом случае истечение газа называют эффузионным, во втором - гидродинамическим. При гидродинамическом истечении макроскопические области газа под действием разности сил давления от примыкающих областей приобретают скорость как целое. Поскольку других молекул, проникающих через перегородку, не существует, то относительные концентрации молекул, собирающихся в специальном резервуаре за время Dt, будут равны Можно теперь применить полученные в данном разделе результаты для выражения коэффициента диффузии (20) через макроскопические параметры:
|

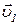 и
и  , а скорости после столкновения
, а скорости после столкновения  и
и  . Нас интересует, энергия, передаваемая от одной молекулы к другой в результате столкновения.
. Нас интересует, энергия, передаваемая от одной молекулы к другой в результате столкновения. и
и  . (21)
. (21) 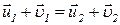 . (22)
. (22)  .] (23)
.] (23) 
 (24)
(24)  - (25)
- (25)  , (26)
, (26) ,
,  – начальные значения энергии молекул. При столкновении одинаковых молекул формула (26) принимает особенно простой вид
– начальные значения энергии молекул. При столкновении одинаковых молекул формула (26) принимает особенно простой вид  . Начальные скорости всех молекул должны иметь беспорядочные направления, так что косинус угла между
. Начальные скорости всех молекул должны иметь беспорядочные направления, так что косинус угла между  . Таким образом, из (26) следует, что в состоянии равновесия
. Таким образом, из (26) следует, что в состоянии равновесия  вне зависимости от соотношения масс молекул. Этот важный результат показывает, что средние кинетические энергии как одинаковых так и разных молекул в веществе одинаковы.
вне зависимости от соотношения масс молекул. Этот важный результат показывает, что средние кинетические энергии как одинаковых так и разных молекул в веществе одинаковы. , (28)
, (28)  . (29)
. (29)  и
и  концентрации молекул обоих типов в откачиваемой камере. Чему равно отношение
концентрации молекул обоих типов в откачиваемой камере. Чему равно отношение 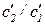 ?
?  для молекул, собранных в камере после просачивания. Выразите это отношение через начальное отношение концентраций.
для молекул, собранных в камере после просачивания. Выразите это отношение через начальное отношение концентраций.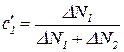 ,
,  . (30)
. (30)  n1S v x1Dt, (31)
n1S v x1Dt, (31)  . (33)
. (33)  , (34)
, (34)  (35)
(35)  , (36)
, (36)  . (37)
. (37) 
 . (38)
. (38)  ,
,  (39)
(39) 
 (40)
(40)  . (41)
. (41)  .
.  . (42)
. (42)


