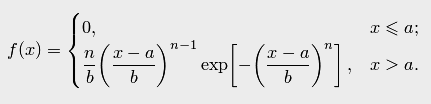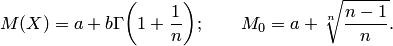Пусть случайная величина  равна отношению двух независимых случайных величин
равна отношению двух независимых случайных величин  и
и  , то есть
, то есть
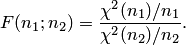
Распределение случайной величины  называется распределением Фишера с
называется распределением Фишера с  и
и 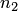 степенями свободы. Оно имеет следующую плотность вероятности
степенями свободы. Оно имеет следующую плотность вероятности
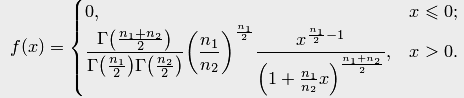
Математическое ожидание случайной величины, подчинённой распределению Фишера,  определяется по формуле
определяется по формуле
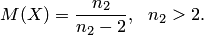
Между случайными величинами, имеющими нормальное распределение: хи-квадрат, Стьюдента и Фишера, имеют место соотношения
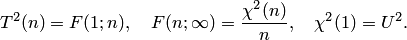
Распределение хи-квадрат 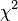
Частный случай гамма-распределения с параметрами  и
и  называется распределением хи-квадрат с
называется распределением хи-квадрат с  степенями свободы (пишут
степенями свободы (пишут  ). Если случайная величина
). Если случайная величина 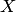 подчиняется закону
подчиняется закону  , то её плотность распределения вероятностей есть
, то её плотность распределения вероятностей есть
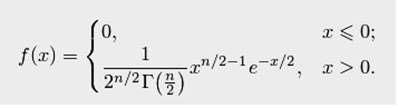
Основные характеристики распределение хи квадрат (математическое ожидание и дисперсия):

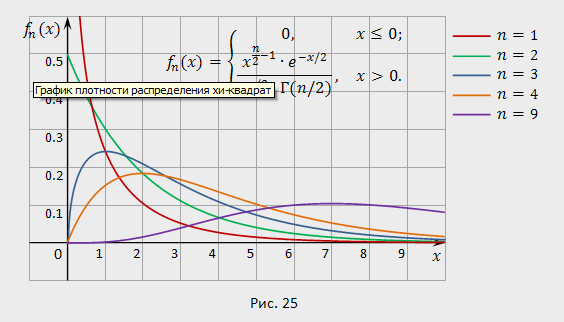
Кривые распределения (для различных значений  ) изображены на рис. 25.
) изображены на рис. 25.
Случайная величина  , подчиняющаяся хи-квадрат распределению, равна сумме квадратов
, подчиняющаяся хи-квадрат распределению, равна сумме квадратов  независимых случайных величин
независимых случайных величин  , каждая из которых имеет стандартизированное нормальное распределение, то есть
, каждая из которых имеет стандартизированное нормальное распределение, то есть
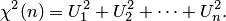
Пусть  и
и  — независимые случайные величины, имеющие хи-квадрат распределение со степенью свободы соответственно
— независимые случайные величины, имеющие хи-квадрат распределение со степенью свободы соответственно  и
и 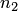 . Сумма этих случайных величин имеет также хи-квадрат распределение с
. Сумма этих случайных величин имеет также хи-квадрат распределение с  степенями свободы:
степенями свободы:
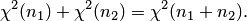
Заметим, что распределение  при больших значениях
при больших значениях  с достаточной для практических расчётов точностью аппроксимируется нормальным распределением с математическим ожиданием
с достаточной для практических расчётов точностью аппроксимируется нормальным распределением с математическим ожиданием  и дисперсией
и дисперсией  . Поэтому при больших значениях
. Поэтому при больших значениях  вероятности рассчитываются по нормальному закону.
вероятности рассчитываются по нормальному закону.
Распределение  играет большую роль в математической статистике.
играет большую роль в математической статистике.
Распределение Вейбула
Случайная величина 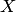 подчиняется закону распределения Вейбула с параметрами
подчиняется закону распределения Вейбула с параметрами  , если её плотность распределения вероятностей записывается в виде
, если её плотность распределения вероятностей записывается в виде
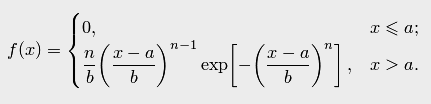
Математическое ожидание и мода случайной величины, распределённые по закону Вейбула, имеют следующий вид:
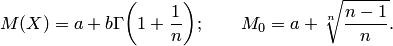
Кривая распределения Вейбула изображена на рис. 22.
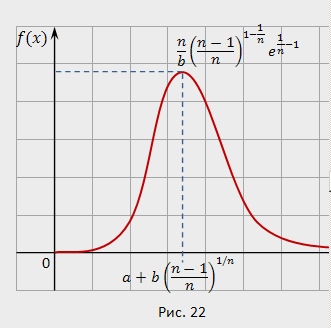
Распределение Вейбула в ряде случаев характеризует срок службы радиоэлектронной аппаратуры и, кроме того, применяется для аппроксимации различных несимметричных распределений в математической статистике.

 равна отношению двух независимых случайных величин
равна отношению двух независимых случайных величин  и
и  , то есть
, то есть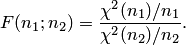
 и
и 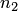 степенями свободы. Оно имеет следующую плотность вероятности
степенями свободы. Оно имеет следующую плотность вероятности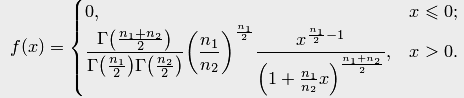
 определяется по формуле
определяется по формуле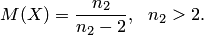
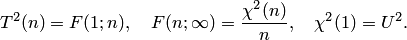
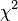
 и
и  называется распределением хи-квадрат с
называется распределением хи-квадрат с  степенями свободы (пишут
степенями свободы (пишут  ). Если случайная величина
). Если случайная величина 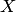 подчиняется закону
подчиняется закону 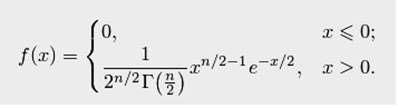


 , подчиняющаяся хи-квадрат распределению, равна сумме квадратов
, подчиняющаяся хи-квадрат распределению, равна сумме квадратов  , каждая из которых имеет стандартизированное нормальное распределение, то есть
, каждая из которых имеет стандартизированное нормальное распределение, то есть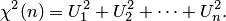
 и
и  — независимые случайные величины, имеющие хи-квадрат распределение со степенью свободы соответственно
— независимые случайные величины, имеющие хи-квадрат распределение со степенью свободы соответственно  степенями свободы:
степенями свободы: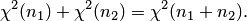
 с достаточной для практических расчётов точностью аппроксимируется нормальным распределением с математическим ожиданием
с достаточной для практических расчётов точностью аппроксимируется нормальным распределением с математическим ожиданием  . Поэтому при больших значениях
. Поэтому при больших значениях  , если её плотность распределения вероятностей записывается в виде
, если её плотность распределения вероятностей записывается в виде