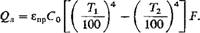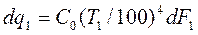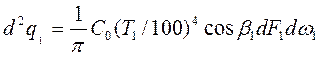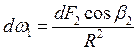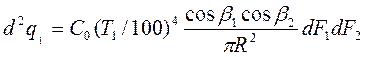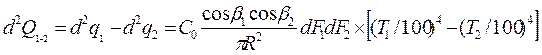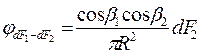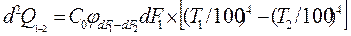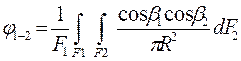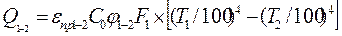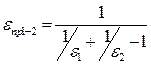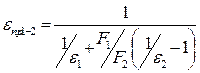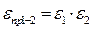ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ
Яндекс.Директ
Особенностью теплообмена излучением является то, что такой теплообмен не требует непосредственного контакта тел. Излучение рассматривается как процесс распространения электромагнитных волн, испускаемых телом. Излучение энергии сводится к преобразованию внутренней энергии тела в лучистую энергию электромагнитных колебаний. Излучение электромагнитных волн свойственно всем телам. Спектр излучения большинства твердых и жидких тел сплошной, непрерывный. Это значит, что эти тела обладают способностью Суммарное излучение с поверхности тела по всем длинам волн спектра называется интегральным или полным лучистым потоком. При постоянной плотности интегрального излучения Е излучающей поверхности полный лучистый поток Q (Вт) определяется в соответствии с (2.8) соотношением Q = EF. (2.336) В общем случае тело, на которое падает лучистый поток, частично поглощает его, частично отражает и частично пропускает (рис. 2.62). На основании закона сохранения энергии можно написать: <2пад = Qa + Qr + Qd Или для плотностей излучения ■Епад = Еа + Er + Ed - (2.337) В безразмерном виде А + R + D = 1. (2.338) Здесь А = Е А / Е Мд называется коэффициентом поглощения; R = — E R / Епод — коэффициент отражения; D = E D/Епад — коэффициент проницаемости. Коэффициенты поглощения, отражения и проницаемости зависят от природы тел, состояния их поверхности. Как видно из формулы (2.331), их значения могут изменяться в пределах от 0 до 1. Тело, которое полностью поглощает всю падающую на него лучистую энергию, следовательно, для которого А — 1, R = D = 0, называют Абсолютно черным телом. Если R = 1, А = D = 0, то такое тело называют абсолютно белым телом, а если D — I, А = R = 0 — абсолютно прозрачным (диатермическим) телом. В дальнейшем все величины, относящиеся к абсолютно черному телу, будут обозначаться индексом «0», например А0 — 1. В природе абсолютно черных, белых и прозрачных тел не существует. Наиболее близки к абсолютно черному телу сажа и бархат (А = 0,97... 0,98), к абсолютно белому телу — полированные металлы (R — 0,97). Одно - и двухатомные газы практически диатермичны. У большинства твердых и жидких тел поглощение тепловых лучей воспринимается лишь поверхностными слоями и для них D = 0, а А + R= 1. Тела, у которых коэффициент поглощения 0 < А < 1 и поглощательная способность не зависит от длины волны падающего излучения, называются серыми телами. Большинство твердых тел можно рассматривать как серые тела. Тела, которые излучают и поглощают лучи только в определенных диапазонах длин волн, обладают так называемым селективным (избирательным) излучением. Для них A =f(k, О - К их числу относятся, например, многоатомные газы (трехатомные и более). Общая энергия, излучаемая телом, состоит из двух составляющих: собственного излучения Е, зависящего от физической природы тела и его температуры, и отраженной лучистой энергии ER. Сумма собственного и отраженного излучений носит название эффективного излучения (рис. 2.63): £Эф = Е + Er = Е + REm!L = Е 4- (1 — А) Е„ад =
- 1) = Е + ЕА
Для абсолютно черного тела А = 1 и, следовательно, £Эф = £ = Неэффективное излучение тел может быть измерено соответствующими приборами — радиометрами, актинометрами и др. Лучистый перенос теплоты характеризуется результирующим излучением Ер, которое определяется разностью между собственным излучением Е и поглощенным лучистым потоком Епогл = АЕпш Ер = Е — АЕтд. (2.340) Результирующее излучение £р также может быть определено в соответствии с (2.339) и (2.340) как разность эффективного и падающего излучений: Ер == Е-) ф £пад - (2.341) Основные законы теплового излучения. Излучение абсолютно черного тела подчиняется следующим законам, которые подробнее изложены в курсе физики. Закон Планка, устанавливающий зависимость между интенсивностью излучения J о, длиной волны X и термодинамической температурой Т:
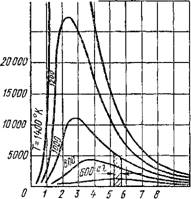
DE0 Сі (2.342) DX Exp ЕР = £ГАЕ2Ц12_ § I Рис. 2.63. К определению видов теплового излучения Как видно из формулы (2.342) и рис. 2.64, при X — 0 и X оо, так же как и при Т= 0, интенсивность излучения J0 = 0. Поэтому при Т— const и некотором значении Хт интенсивность излучения достигает максимума. Закон Вина исходя из закона Планка дает зависимость между Хт и Т. ХтТ= 2,9-10" 3. (2.343) Как видно из формулы (2.343), с повышением температуры длина волны, соответствующая максимальной интенсивности излучения, смещается в сторону более коротких длин воли. Закон Стефана— Больцмана дает возможность определить плотность лучистого потока £0 абсолютно черного тела путем интегрирования уравнения (2.342). Этот закон был установлен И. Стефаном экспериментально в 1879 г. и JI. Больцманом теоретически в 1884 г. Исходя из закона Планка, можно доказать, что £0 пропорциональна четвертой степени абсолютной температуры: E0 = ^J0dX = а0Т (2.344) Где ст0 = 5,67 • 10" 8 ВтДм2 • К4) — константа излучения абсолютно черного тела. В технических расчетах закон Стефана — Больцмана удобно применять в форме Е0 = Со (Т/100)4, Где Со = ст0* 108 = 5,67 ВтДм2 • К4) — коэффициент излучения абсолютно черного тела. Для серых тел, у которых интенсивность излучения меньше, чем у черных тел при той же температуре, Е < £0. Отношение £/£0 < 1 называют степенью черноты серого тела є = £/£0. Пользуясь понятием о степени черноты, плотность лучистого потока для серого тела можно выразить следующим уравнением: Е = sЈo — єС0 (Т/100)4 = С (Г/100)4, (2.345) Где С = еС0 — коэффициент излучения серого тела. Закон Кирхгофа устанавливает связь между излучательной и поглощательной способностью тел. Для вывода этой зависимости составим баланс лучистого теплообмена между параллельно расположенными неограниченными серой 1 и абсолютно черной 2 пластинами (рис. 2.65). Примем вначале Т>; Т0. Тогда количество теплоты, передаваемой серым телом черному, Ер = Е — Еа = Е — ЕоА. (2.346) В частном случае, при равенстве температур тел, участвующих в лучистом теплообмене (Т= Т0), имеет место тепловое равновесие, при котором Ер — 0. При этом на основании формулы (2.346) Е — Е0А = 0, или Е/А = Е0. (2.347) Уравнение (2.347) составляет содержание закона Кирхгофа: отношение энергии излучения тела к его поглощательной способности для всех тел одинаково и равно энергии излучения абсолютно черного тела при той же температуре. Уравнение (2.347) может быть преобразовано следующим образом: А = Е/Е0 = £, (2.348) Т. е. коэффициент поглощения численно равен степени черноты данного тела. Закон Ламберта дает возможность определить зависимость изменения энергии лучистого потока от его направления по отношению к поверхности тела. Наибольшей интенсивностью обладает излучение по нормали к поверхности Еп. По остальным направлениям оно меньше, равно £,,, и выражается формулой £ф = Еп cos ф, (2.349) Где ср — угол между направлением излучения и нормалью (рис. 2.66). Из закона Ламберта следует, что плотность полусферического излучения в пределах телесного угла со = 2тс: Е = Е„к, откуда Е„ = Е/к, Где Е — плотность интегрального полусферического излучения, определяемого по закону Стефана — Больцмана по формуле (2.345); Е„ — плотность излучения по нормали. Соответственно по направлению <р плотность излучения определяется по формуле (2.349), или после подстановки Е„: £ф = (Е/л) cos <р.
Лучистый теплообмен между телами. Рассмотрим стационарный лучистый теплообмен между телами 1 и 2 (рис. 2.67) при условии, что эти тела образуют замкнутую систему, лучистый теплообмен происходит только между ними и степень черноты этих тел не зависит от температуры. Рис. 2.66. К выводу закона Ламберта Обозначим температуру, поверхность и степень черноты более нагретого тела Ті, F І и єь а менее нагретого тела — Т2, F2 и є2 соответственно. При произвольном расположении в пространстве тел, участвующих в лучистом теплообмене, не вся лучистая энергия, излучаемая одним телом, падает на другое. Доля полного лучистого потока одного тела, которая попадает на другое тело, называется угловым коэффициентом излучения, или коэффициентом облученности ф. Для двух тел, участвующих в лучистом теплообмене, коэффициент облученности первого тела Фі2 = 612/Q1; (2.350) Второго Фаі-бзі/ба. (2-351) При равных температурах двух абсолютно черных тел, участвующих в лучистом теплообмене, (212 = <2зь Найдем значения Q12 и Q2 1 из уравнений (2.336), (2.350) и (2.351): QI2 = Фіг^іЕзфі; 621 = Ф2і^2£3ф2- Но для абсолютно черных тел при одинаковых температурах эффективное излучение равно собственному £3фі = £Эф2 = EQ, тогда Фі2^ = ф21£2 = £л. (2.352) Уравнение (2.352) называется уравнением взаимности, a Fn называется лучевоспринимающей или взаимной поверхностью. По уравнению (2.352) взаимная (лучевоспринимающая) поверхность пары тел равна произведению площади поверхности одного из тел на угловой коэффициент излучения от этого тела на другое. Понятием взаимной поверхности пользуются при расчетах лучистого теплообмена. Результирующий лучистый тепловой поток от первого тела на второе: 6л = Ф12^эф1^1 - Ф21£эф2^2 = (-Еэф1 - £эф2)£л - (2.353) Подставив значения эффективного излучения (2.339) для первого тела
£Эф1 = Е + Елі — и для второго £Эф2 — Е2 + £д2^— 1 ^J, получим Fa. (2.354) Єї J ' s2 Исключим из уравнения (2.354) величины Еа І И £л2- Для этого напишем значение Qn для каждого из тел, участвующих в теплообмене: Для первого тела
<2л = (£і - EAi)Fr, (2.355)
Для второго тела
Qn = (Ea2-E2)F2. Решая совместно (2.354), (2.355) и (2.356), находим Е! <2л = Є2У L i^l V Є1 / F262 После подстановки значений Еі = єхСо (71/100)4 и Е2 = Є2С0 (Т2/100)4, а также значений угловых коэффициентов срі2 и ф2і в уравнение (2.357) получим
Окончательно получим расчетную формулу для определения количества теплоты, передаваемой одним телом другому путем излучения:
Qji — ЄПпСо Величина єпр называется приведенной степенью черноты замкнутой системы двух серых тел. Полученное выражение (2.360) является общей формулой для замкнутой системы двух серых тел, произвольно расположенных в пространстве. Применим эту формулу для ряда частных случаев: а) 1-е тело, не имеющее вогнутостей, находится внутри 2-го и все его эффективное излучение полностью падает на 2-е тело (рис. 2.68). Тогда фіг = 1, а согласно формуле (2.352) Fn = Ft = ф2і£2 и, следовательно, Ф21 = F1/F2■; Поэтому для этого случая V = ------------ ЇГ^ГЇ--------- г, (2.361) 1 Fx — 4----- L 81 F 2
А 6л — епр^0
Б) тот же случай, но при Fі <§; F2. При этих условиях согласно формуле (2.361) имеем є„р % єь т. е. приведенная степень черноты определяется степенью черноты меньшего тела;
В) оба тела представляют собой параллельные неограниченные пластины. В этом случае Фіг = Ф21 = 1, F = F2 = F, а приведенная степень черноты согласно формулам (2.359) и (2.361): £пр " 1/si + 1/є2 - 1 ' А (2.363) Методы изменения интенсивности лучистого теплообмена между телами. Основное уравнение лучистого теплообмена между телами (2.360) показывает, что для интенсификации лучистого теплообмена необходимо увеличить степень черноты тел, температуру излучающего тела Ті, а также применять такое расположение тел, чтобы увеличить угловой коэффициент ф12. По мере увеличения температуры нагреваемого тела Т2 интенсивность лучистого теплообмена между телами снижается. В качестве эффективного мероприятия для уменьшения лучистого теплообмена между телами применяется установка между ними экранов. Последние представляют собой тонкие листы, перепадом температур по толщине которых можно пренебречь. Рассмотрим влияние экранов на уменьшение теплообмена между двумя параллельными пластинами, температуры которых обозначим 71 и Т2, а степень черноты =е2 = £э (рис. 2.69). Для упрощения вывода примем, что все экраны, число которых обозначим через п, имеют ту же степень черноты є, что и пластины. При стационарном тепловом режиме плотность лучистого потока энергии между пластинами и экранами будет одинакова, т. е.
HX
100 У Э(п - T) 100 100/ HlY
100 у Где є„р вычисляется по формуле (2.362). При п экранах число таких равенств будет равно п + 1. Складывая их почленно, получим выражение, в котором все промежуточные температуры экранов взаимно сократятся, т. е. (n+l)q3 = єпрСо [(Ті/100)4 - (Г2/100)4]. Отсюда плотность лучистого потока при установке экранов
При отсутствии экранов плотность того же потока будет Q = єпрСо [(7І/100)4 - (7І/100)4]. (2.366) Следовательно, при установке п экранов плотность лучистого потока уменьшается в п + 1 раз. Решая совместно (2.365) и (2.366), получим Зэ = Q/(N + 1). (2.367) Как видно из формулы (2.365), лучистый теплообмен между телами зависит как от числа экранов и, так и от приведенной степени черноты ЕПр. Согласно формуле (2.363) последняя уменьшается с уменьшением степени черноты экранов. Поэтому, выбрав экраны с очень малой є (из хорошо отполированного металла), можно резко сократить число необходимых экранов. Температура экранных поверхностей может быть определена из уравнения (2.364), после того как по формуле (2.365) подсчитана величина <2Э. В частности, при установке одного экрана
(2.368) Экраны применяются для повышения термического сопротивления ограждающих конструкций зданий и транспортных устройств, а также при изоляции тепловых аппаратов и приборов. Суммируя изложенное выше, тепловое излучение поверхностей в помещении в дальнейшем будем рассматривать как инфракрасное монохроматическое диффузное, подчиняющееся законам Стефана-Больцмана, Ламберта и Кирхгофа - излучение поверхностей серых тел. Воздух помещения при расчете лучистого теплообмена между поверхностями можно считать лучепрозрачной средой. Он состоит в основном из двухатомных газов (азот, кислород), которые совершенно прозрачны для тепловых лучей и сами не излучают тепловой энергии. Незначительное содержание многоатомных газов (водяной пар и углекислота) при малых толщинах слоя воздуха в помещении практически не изменяет этого свойства.
Каждая поверхность отдает тепло излучением и поглощает лучистое тепло, приходящее от окружающих поверхностей. Нагретые поверхности теряют больше тепла, чем поглощают. Более Холодные, наоборот, получают больше тепла, чем отдают. Между различно нагретыми поверхностями в результате происходит теплообмен излучением.
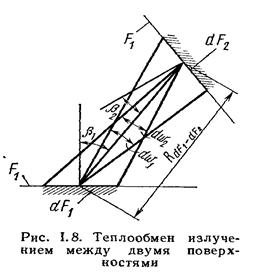
Рассмотрим вначале теплообмен излучением между двумя абсолютно черными поверхностями 1 и 2. В соответствии с законом Стефана-Больцмана, элементарная площадка dF1 на поверхности 1 излучает во все направления в пределах полусферы количество тепла, равное
Интенсивность излучения в направлении, нормальном К поверхности dF1, в π раз меньше dq1, т. е.
Интенсивность излучения под углом β1 к нормали (в направлении к элементарной Площадке dF2) равна
в пределах телесного угла dω1 излучение тепла равно
Телесный угол dω1, определяемый dF2, равен
где dF2cosβ2 -проекция площадки dF2 на сферу радиусом R с центром в dFl, когда угол между направлением излучения и нормалью к поверхности dF2 равен β2; R - расстояние между элементарными площадками dFl и dF2. Уравнение можно записать
Аналогичное уравнение может быть написано для потока тепла d2q2 передаваемого площадкой dF2 в сторону dFl. В результате лучистого теплообмена от площадки dF1 передается площадке dF2 количество тепла, равное
Удобно воспользоваться понятием коэффициента облученности φ, который является геометрической характеристикой. Коэффициент облученности с площадки dFl на dF2 равен отношению лучистого потока, падающего с dFl на dF2 ко всему потоку, излучаемому dFl, т. е.
Теплообмен излучением между двумя поверхностями 1 и 2, полные площади которых равны Fl на F2, можно получить двойным интегрированием уравнения по площадям Fl и F2.
Где коэффициент облученности φ1-2 с поверхности 1 на поверхность 2 равный
показывает долю лучистого потока, попадающую на поверхность 2, от всего потока, излучаемого поверхностью 1. Поверхности в помещений отличаются от абсолютно черных, что осложняет задачу, так как падающая на серую поверхность лучистая энергия частично отражается. Некоторая ее часть может многократно отражаться от взаимно облучаемых серых поверхностей, пока полностью ими не поглотится. Из теории лучистого теплообмена известно, что при теплообмене монохроматическим излучением двух серых поверхностей, для которых справедливы законы Ламберта и Кирхгофа, количество переданного тепла определяется по формуле
где εпр1-2 есть приведенный относительный коэффициент излучения при теплообмене между двумя серыми поверхностями. Для определения εпр1-2 можно рассмотреть три простейших случая: 1. Для двух параллельных поверхностей, расстояние между которыми мало по сравнению с их размерами
2. Поверхность со всех сторон окружена другой поверхностью. Это сфера в сфере, цилиндр в цилиндре или просто невогнутая поверхность, окруженная большей поверхностью такой же геометрии
3. Если поверхности малы или велико расстояние между ними, то часть отраженного излучения, возвращающаяся на излучающую поверхность, становится пренебрежимой. В этом случае
|

 Рис. 2.61. График для определения поправочного коэффициента к, к формуле (2.335)
Рис. 2.61. График для определения поправочного коэффициента к, к формуле (2.335)
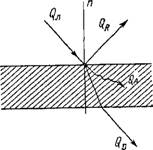 Рис. 2.62. Распределение лучистого теплового потока, падающего на тело
Рис. 2.62. Распределение лучистого теплового потока, падающего на тело
 30000------------
30000------------
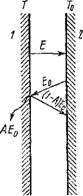 Рис. 2.65. К
Выводу закона Кирхгофа
Рис. 2.65. К
Выводу закона Кирхгофа
 Рис. 2.67. Лучистый теплообмен между телами в замкнутой системе
Рис. 2.67. Лучистый теплообмен между телами в замкнутой системе
 Рис. 2.69. Лучистый теплообмен при наличии экранов
Рис. 2.69. Лучистый теплообмен при наличии экранов