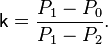Адиабатический процесс. Уравнение Пуассона для адиабатического процесса. Показатель адиабаты.
Адиабатический, процесс — термодинамический процесс в макроскопической системе, при котором система не обменивается теплотой с окружающим пространством. Адиабатические процессы обратимы только тогда, когда в каждый момент времени система остаётся равновесной (например, изменение состояния происходит достаточно медленно) и изменения энтропии не происходит. Обратимый адиабатический процесс для идеального газа описывается уравнением Пуассона. Линия, изображающая адиабатный процесс на термодинамической диаграмме, называется адиабатой Пуассона. Примером необратимого адиабатического процесса может быть распространение ударной волны в газе. Такой процесс описывается ударной адиабатой. Если термодинамический процесс в общем случае являет собой три процесса — теплообмен, совершение системой (или над системой) работы и изменение её внутренней энергии, то адиабатический процесс в силу отсутствия теплообмена (
где Изменения энтропии S системы в обратимом адиабатическом процессе вследствие передачи тепла через границы системы не происходит:
Здесь Адиабата Пуассона Для идеальных газов, чью теплоёмкость можно считать постоянной, в случае квазистатического процесса адиабата имеет простейший вид и определяется уравнением
где
График адиабаты (жирная линия) на диаграмме для газа. С учётом уравнения состояния идеального газа уравнение адиабаты может быть преобразовано к виду
где
Поскольку При адиабатическом процессе показатель адиабаты равен Для нерелятивистского невырожденного одноатомного идеального газа Для реальных газов показатель адиабаты отличается от показателя адиабаты для идеальных газов, особенно для низких температур, когда большую роль начинает играть межмолекулярное взаимодействие. Один из методов для экспериментального определения показателя был предложен в 1819 г. Клеманом и Дезормом. Стеклянный баллон вместимостью несколько литров наполняется исследуемым газом при давлении
|

 ) системы со средой сводится только к последним двум процессам. Поэтому, первое начало термодинамики в этом случае приобретает вид
) системы со средой сводится только к последним двум процессам. Поэтому, первое начало термодинамики в этом случае приобретает вид
 — изменение внутренней энергии тела,
— изменение внутренней энергии тела, 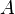 — работа, совершаемая системой.
— работа, совершаемая системой.
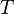 — температура системы,
— температура системы,  — теплота, полученная системой. Благодаря этому адиабатический процесс может быть составной частью обратимого цикла.
— теплота, полученная системой. Благодаря этому адиабатический процесс может быть составной частью обратимого цикла.
 — его объём,
— его объём,  — показатель адиабаты,
— показатель адиабаты,  и
и  — теплоёмкости газа соответственно при постоянном давлении и постоянном объёме.
— теплоёмкости газа соответственно при постоянном давлении и постоянном объёме.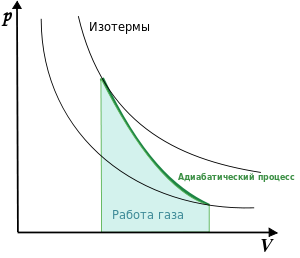
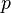 — давление газа;
— давление газа; 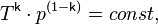

 всегда больше 1, из последнего уравнения следует, что при адиабатическом сжатии (то есть при уменьшении
всегда больше 1, из последнего уравнения следует, что при адиабатическом сжатии (то есть при уменьшении  .
. , для двухатомного
, для двухатомного 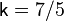 , для трёхатомного
, для трёхатомного  , для газов, состоящих из более сложных молекул, показатель адиабаты
, для газов, состоящих из более сложных молекул, показатель адиабаты  .
. Затем открывается кран, газ адиабатически расширяется, и давление падает до атмосферного —
Затем открывается кран, газ адиабатически расширяется, и давление падает до атмосферного —  . Затем происходит его изохорное нагревание до температуры окружающей среды. Давление повышается до
. Затем происходит его изохорное нагревание до температуры окружающей среды. Давление повышается до  . В результате такого эксперимента k можно вычислить как
. В результате такого эксперимента k можно вычислить как