Статистический вес и энтропия. Закон возрастания энтропии. Равновесные и неравновесные состояния.
Термодинамической вероятностью или статистическим весом макросостояния W - называется число микросостояний, осуществляющих данное макросостояние (или число перестановок одноименных элементов, при которых сохраняется данное макросостояние). Термодинамическая вероятность W - максимальна, когда система находится в равновесном состоянии. В состоянии равновесия и термодинамическая вероятность максимальна, и энтропия максимальна. Понятие энтропии впервые было введено для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Энтропия S – аддитивная величина: Вероятность сложного события, есть произведение вероятностей состояний:
где W1 – первое состояние; W2 – второе состояние. Аддитивной величиной является логарифм термодинамической вероятности:
Поэтому Л. Больцман предложил:
где k – коэффициент Больцмана. С этой точки зрения энтропия выступает, как мера беспорядочности, хаотичности состояния. Связь между S и W позволяет несколько иначе сформулировать второе начало термодинамики: наиболее вероятным изменением энтропии является ее возрастание. Энтропия – вероятностная статистическая величина. Утверждение о возрастании энтропии потеряло свою категоричность. Её увеличение вероятно, но не исключаются флуктуации. Л. Больцман один из первых опроверг эту гипотезу и показал, что закон возрастания энтропии – статистический закон, т.е. возможны отклонения. Энтропия замкнутой системы – максимальна, при достижении системой равновесного состояния. Макроскопическая система, состоящая из большого числа частиц (N ~ NA), согласно эргодической гипотезе проводит одинаковое время во всех своих микросостояниях. В результате с большей вероятностью реализуются макросостояния с наибольшим статистическим весом, в этих макросостояниях система проводит большую часть своего времени. Иногда система случайным образом оказывается в макросостояниях с меньшим статвесом, но так как статвес их мал, проводит в них незначительную часть своего времени. При этом физические величины, характеризующие систему, испытывают кратковременные отклонения от своих средних значений. Такие отклонения называются флуктуациями. Равновесным называется такое макроскопическое состояние системы, которое не имеет тенденции к изменению с течением времени. Ясно, что равновесное макросостояние - это такое состояние, которое реализуется наибольшим числом микросостояний, т.е. статвес равновесного состояния максимален. Неравновесные состояния - это состояния со статвесом меньшим, чем у равновесного. В неравновесном состоянии система находится тем меньше, чем меньше его статвес.
|

 , где
, где  - сумма энтропий тел, входящих в систему.
- сумма энтропий тел, входящих в систему.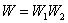 ,
,
 .
.
 ,
,



