Распределение частиц идеального газа по абсолютному значению скорости. Вероятная, средняя и среднеквадратичная скорости молекул.
Закон распределения молекул идеального газа по скоростям, теоретически полученный Максвеллом в 1860 г. определяет, какое число dN молекул однородного (p = const) одноатомного идеального газа из общего числа N его молекул в единице объёма имеет при данной температуре Т скорости, заключенные в интервале от v до v + dv. Для вывода функции распределения молекул по скоростям f(v) равной отношению числа молекул dN, скорости которых лежат в интервале v ÷ v + dv к общему числу молекул N и величине интервала dv
Максвелл использовал два предложения: а) все направления в пространстве равноправны и поэтому любое направление движения частицы, т.е. любое направление скорости одинаково вероятно. Это свойство иногда называют свойством изотропности функции распределения. б) движение по трем взаимно перпендикулярным осям независимы т.е. х-компоненты скорости Считается также, что газ состоит из очень большого числа N тождественных молекул находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Силовые поля на газ не действуют. Функции f (v) определяет относительное число молекул dN(v)/N скорости которых лежат в интервале от v до v + dv (например: газ имеет N = 106 молекул, при этом dN = 100 молекул имеют скорости от v =100 до v + dv =101 м/с (dv = 1 м/с) тогда Используя методы теории вероятностей, Максвелл нашел функцию f (v) - закон распределения молекул идеального газа по скоростям:
f (v) зависит от рода газа (от массы молекулы) и от параметра состояния (от температуры Т) f(v) зависит от отношения кинетической энергии молекулы, отвечающей рассматриваемой скорости
<X>= Тогда средняя арифметическая скорость молекул
и интегрируя по частям получили
Скорости, характеризующие состояние газа: 1. Наиболее вероятная скорость,
2. Средняя скорость
3. Среднеквадратичная скорость
|


 не зависит от того каково значения ее компонент
не зависит от того каково значения ее компонент  или
или  . И тогда вывод f (v) делается сначала для одной компоненты
. И тогда вывод f (v) делается сначала для одной компоненты 

 к величине kT характеризующей среднюю тепловую энергию молекул газа.
к величине kT характеризующей среднюю тепловую энергию молекул газа. При малых v
При малых v  и функция f(v) изменяется практически по параболе
и функция f(v) изменяется практически по параболе  . При возрастании v множитель
. При возрастании v множитель  уменьшается быстрее, чем растет множитель
уменьшается быстрее, чем растет множитель 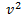 , т.е. имеется max функции f(v). Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью
, т.е. имеется max функции f(v). Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью  найдем из условия
найдем из условия


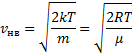
 , следовательно, с ростом температуры наиболее вероятная скорость растёт, но площадь S, ограниченная кривой функции распределения остаётся неизменной, так как из условия нормировки
, следовательно, с ростом температуры наиболее вероятная скорость растёт, но площадь S, ограниченная кривой функции распределения остаётся неизменной, так как из условия нормировки  (так как вероятность достоверного события равна 1), поэтому при повышении температуры кривая распределения f (v) будет растягиваться и понижаться.
(так как вероятность достоверного события равна 1), поэтому при повышении температуры кривая распределения f (v) будет растягиваться и понижаться. В статистической физике среднее значение какой-либо величины определяется как интеграл от 0 до бесконечности произведения величины на плотность вероятности этой величины (статистический вес)
В статистической физике среднее значение какой-либо величины определяется как интеграл от 0 до бесконечности произведения величины на плотность вероятности этой величины (статистический вес)


 – вероятность обладания которой любой молекулой системы максимальна, и которая соответствует максимальному значению
– вероятность обладания которой любой молекулой системы максимальна, и которая соответствует максимальному значению  Чтобы найти её, необходимо вычислить
Чтобы найти её, необходимо вычислить  , приравнять её нулю и решить относительно
, приравнять её нулю и решить относительно 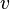 :
: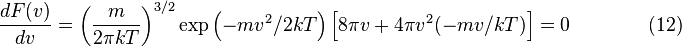

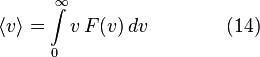 Подставляя
Подставляя 
 Подставляя
Подставляя 



