Развитие творческого мышления
Пересечение кривой второго порядка и прямой. Асимптотические направления. Литература. [1]§ 32.
Под кривой второго порядка понимается множество точек, координаты которых в некоторой аффинной системе координат являются решениями алгебраического уравнения второго порядка с двумя неизвестными:
где коэффициенты Пусть даны кривая второго порядка g своим общим уравнением (*) и прямая l, проходящая через точку
Заменим значения х и у в уравнении g на их выражения (1), а затем решим полученное уравнение относительно параметра t. Найденные корни будут параметрами точек пересечения g и l.
После преобразований получим:
Если P ¹ 0, то (2) представляет собой квадратное уравнение, у которого либо два действительных, либо один, либо два комплексно сопряженных корня. Поэтому g и l либо имеют две общие точки, либо одну или, как говорят, две совпавшие вещественные точки, либо ни одной вещественной, но, как принято говорить, две так называемые комплексно сопряженные точки. Если Из формулы (3) следует, что коэффициент Р уравнения (2) не зависит от координат начальной точки прямой. Он является однородным многочленом второго порядка от координат a и b направляющего вектора прямой. Поэтому, если координаты некоторого вектора Определение 1. Прямая l называется прямой асимптотического направления кривой g, если координаты любого ее направляющего вектора обращают коэффициент Р уравнения (2) в нуль. Легко объяснить, если координаты направляющего вектора прямой обращая в нуль коэффициент Р в некоторой системе координат, то координаты этого вектора будут также обладать таким свойством в любой другой системе координат. Действительно, как было показано выше, прямая имеет асимптотическое направление в том и только в том случае, когда либо не имеет с кривой второго порядка g общих точек, либо имеет только одну такую точку, либо целиком ей принадлежит g. Поэтому свойство прямой иметь асимптотическое направление имеет геометрический смысл, не зависящий от выбора системы координат. Определение 2. Любой направляющий вектор прямой асимптотического направления будем называть вектором асимптотического направления, а множество таких коллинеарных между собой ненулевых векторов ‑ асимптотическим направлением. Из определений 1 и 2, а также из формулы (3) следует, что вектор
Мы получили однородное уравнение второго порядка с неизвестными a и b. Если мы нашли какое-либо его ненулевое решение 1) 2)
Мы получили квадратное уравнение относительно l. Его дискриминант D равен:
Легко видеть, что 3) Число асимптотических направлений кривой зависит от знака числа D. Покажем, что знак и условие равенства нулю этого числа не зависит от выбора аффинной системы координат. Воспользуемся формулами перехода от одной аффинной системы координат к другой:
где
Для определения коэффициентов уравнения кривой в новой системе координат следует в общем уравнение (*) кривой второго порядка заменить неизвестные
при этом:
Отсюда, после соответствующих вычислений получим:
(все вычисления проведите самостоятельно). Равенство нулю определителя D и его знак не зависят от выбора аффинной системы координат на плоскости. Полученный результат можно было предвидеть, так как количество асимптотических направлений является геометрическим свойством кривой второго порядка и оно одинаково в любой системе координат. Доказана теорема: Теорема 1. Кривая второго порядка в том и только в том случае имеет два асимптотических направления, когда в некоторой аффинной системе координат определитель Будем считать, что уравнение кривой мы рассматриваем в прямоугольной декартовой системе координат. Формулы (9) перехода от одной прямоугольной декартовой системы координат к другой имеют вид
где
Таким образом, при переходе от одной прямоугольной декартовой системы координат к другой значение определителя D не меняется. Определитель D носит название первого инварианта кривой второго порядка. Нетрудно определить, что для эллипса первый инвариант D положителен. Для этого достаточно найти этот инвариант в случае канонического уравнения эллипса. Кривые, для которых первый инвариант положителен, называются кривыми эллиптического типа. Такие кривые не имеют асимптотических направлений. Рассмотрим гиперболу, заданную своим каноническим уравнением: Рассмотрим ее каноническое уравнение параболы:
Развитие творческого мышления · Малаховская Наталья Анатольевна, педагог-психолог Разделы: Школьная психологическая служба На современном этапе развития общества четко выражена потребность в специалистах, обладающих высоким уровнем развития творческого потенциала, умеющих системно мыслить, ставить и нестандартно решать различные задачи. В стремительно меняющихся условиях общественного и технического развития особенно важными качествами человека становятся творческая активность, новаторство, нестандартность решений. Задача воспитания людей с творческим складом ума превратилась в назревшую социальную необходимость. Еще в начале века французский психолог Рибо заметил, что оригинальность мышления к 14-ти годам снижается. Значительный регресс творческости у младшего юношества отмечается психологами и в наше время. Поэтому, необходимо постоянно развивать и активизировать творческое мышление учащихся. Исследования ряда психологов показывают, что при соответствующих целенаправленных и систематических усилиях можно получить весьма плодотворные результаты. Творчество следует рассматривать не только как профессиональную характеристику, но и как необходимое личностное качество, позволяющее человеку адаптироваться в быстро меняющихся социальных условиях и ориентироваться во все более расширяющемся информационном поле. Успешность развития творческого системного мышления в процессе профессионального образования во многом определяется уровнем сформированности основных компонентов творческого мышления на более ранних этапах формирования личности. В число таких компонентов входят: - способность к анализу, синтезу, сравнению и установлению причинно-следственных связей; - критичность мышления (обнаружение разного рода ошибок, рассогласований) и способность выявлять противоречия; - прогнозирование возможного развития событий; - способность видеть любую систему или объект в аспекте прошлого, настоящего и будущего; - умение выстраивать алгоритм действия, генерировать новые идеи; - порождать необычные идеи, отклоняться в мышлении от традиционных схем, быстро разрешать проблемные ситуации. Что же такое творческое мышление? Известный американский психолог Э. Фромм определяет его как «способность удивляться, познавать и находить решения в нестандартных ситуациях, …нацеленность на открытие нового и способность к глубокому осознанию своего опыта». Близко к понятию «творческое мышление термины «креативность» и «дивергентное мышление». Под креативностью понимается способность находить в быстром темпе разные способы решения задач. Лежащий в основе этой способности комплекс особенностей мыслительного процесса Дж. Гилфорд назвал дивергентным мышлением. В психологических исследованиях выявлен целый ряд таких особенностей, взаимосвязанных и образующих целую структуру: Быстрота мышления – способность высказывать максимальное число идей за короткий промежуток времени. Гибкость мышления – способность видеть проблему с разных сторон, богатство ассоциативной деятельности, заключающееся в установлении очень далеких ассоциаций, нахождение сходства в явлениях, на первый взгляд ничем не связанных. Оригинальность мышления – своеобразие творческого мышления, необычность подхода к проблеме, способность находить необычные ответы. Синтетичность мышления – способность охватить все проблемное поле одним взглядом. Точность (завершенность) – логичность творческого мышления, выбор адекватного решения, соответствующего поставленной цели. Специфическая природа творческого мышления определяет нетрадиционный характер методик его диагностики и развития. Они обычно не регламентируют деятельность учащихся, не предполагают наличия правильных или неправильных ответов, не ограничивают их числа. Оценивается нестандартность решений, их разнообразие. Ценность этих методик состоит в том, что их можно применять не только для диагностики, но и для развития творческого мышления. Занятия по развитию творческого мышления можно проводить не только индивидуально, но и давая задания на подгруппы, в форме КВН, «мозгового штурма», что вызывает повышенный интерес у учащихся, требует умения договариваться друг с другом, принимать множество решений. В качестве примера предлагаются задания для КВН среди учащихся 14-16 лет, которые можно преобразовывать. Цели и задачи: - стимулирование способности к размышлению; - развитие творческого мышления; - сплочение коллектива; - развитие коммуникативных навыков.
|

 , (*)
, (*) не равны нулю одновременно. Было также показано, что порядок уравнения алгебраической кривой не зависит от выбора системы координат.
не равны нулю одновременно. Было также показано, что порядок уравнения алгебраической кривой не зависит от выбора системы координат.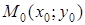 и параллельная вектору
и параллельная вектору  требуется найти их точки пересечения. Рассмотрим параметрические уравнения прямой l:
требуется найти их точки пересечения. Рассмотрим параметрические уравнения прямой l: (1)
(1)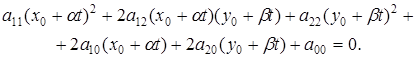
 , (2)
, (2) , (3)
, (3) , (4)
, (4) . (5)
. (5)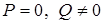 , то уравнение (2) ‑ линейное, оно имеет один вещественный корень. В этом случае прямая и кривая обладают единственной общей точкой. Ясно, что этот случай, по сути, отличается от предыдущего случая двух совпавших вещественных точек. Если
, то уравнение (2) ‑ линейное, оно имеет один вещественный корень. В этом случае прямая и кривая обладают единственной общей точкой. Ясно, что этот случай, по сути, отличается от предыдущего случая двух совпавших вещественных точек. Если  , а R ¹ 0, то уравнение (2) не имеет корней, а g и l - общих точек. И, наконец, если Р = Q = R = 0, то любое значение t - корень уравнения, а прямая l всеми точками принадлежит g.
, а R ¹ 0, то уравнение (2) не имеет корней, а g и l - общих точек. И, наконец, если Р = Q = R = 0, то любое значение t - корень уравнения, а прямая l всеми точками принадлежит g. обращают коэффициент Р в нуль, то он также равен нулю, при подстановке в (3) координат a и b любого вектора, коллинеарного
обращают коэффициент Р в нуль, то он также равен нулю, при подстановке в (3) координат a и b любого вектора, коллинеарного  тогда и только тогда имеет асимптотическое направление, когда он отличен от нулевого и
тогда и только тогда имеет асимптотическое направление, когда он отличен от нулевого и . (6)
. (6) , то все пары чисел
, то все пары чисел  , где
, где  , также служат решениями (6). Поэтому вектор
, также служат решениями (6). Поэтому вектор  определяет асимптотическое направление прямой. Выясним, сколько асимптотических направлений может иметь кривая второго порядка. Для этого найдем число не пропорциональных между собой решений (6).
определяет асимптотическое направление прямой. Выясним, сколько асимптотических направлений может иметь кривая второго порядка. Для этого найдем число не пропорциональных между собой решений (6). . Тогда
. Тогда  и уравнение (6) преобразуется к виду:
и уравнение (6) преобразуется к виду: 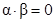 . Оно имеем два не пропорциональных между собой решения: (1; 0) и (0; 1), все решения имеют вид: (t; 0) и (0; t), где t - любое действительное число, отличное от нуля. Кривая имеет два асимптотических направления.
. Оно имеем два не пропорциональных между собой решения: (1; 0) и (0; 1), все решения имеют вид: (t; 0) и (0; t), где t - любое действительное число, отличное от нуля. Кривая имеет два асимптотических направления. . Тогда пара чисел (t; 0), где t ¹ 0, не является решением уравнения (19.6). Действительно, если подставить эти числа в уравнение, то получим противоречивое равенство:
. Тогда пара чисел (t; 0), где t ¹ 0, не является решением уравнения (19.6). Действительно, если подставить эти числа в уравнение, то получим противоречивое равенство:  . В рассматриваемом случае для любого решения
. В рассматриваемом случае для любого решения  уравнения (6) b ¹ 0. Разделив это уравнение на b, мы не потеряем его решений. Обозначим
уравнения (6) b ¹ 0. Разделив это уравнение на b, мы не потеряем его решений. Обозначим  , тогда:
, тогда: . (7)
. (7) . Обозначим через D определитель:
. Обозначим через D определитель: . (8)
. (8) . Таким образом, если D < 0, то уравнение (7) имеет два решения, а кривая g ‑ два асимптотических направления. Если D = 0, то такое направление одно, а в случае D > 0 кривая не имеет асимптотических направлений.
. Таким образом, если D < 0, то уравнение (7) имеет два решения, а кривая g ‑ два асимптотических направления. Если D = 0, то такое направление одно, а в случае D > 0 кривая не имеет асимптотических направлений. , но
, но  для отыскания асимптотических направлений уравнение (6) следует делить на
для отыскания асимптотических направлений уравнение (6) следует делить на  . Аналогично рассуждая, придем к тому же результату: если D < 0 кривая имеет два асимптотических направления, если
. Аналогично рассуждая, придем к тому же результату: если D < 0 кривая имеет два асимптотических направления, если  , то это направление одно, если D > 0, то таких направлений у кривой нет. В первом случае, когда
, то это направление одно, если D > 0, то таких направлений у кривой нет. В первом случае, когда  кривая имела два асимптотических направления, выполнено неравенство:
кривая имела два асимптотических направления, выполнено неравенство:  .
. (9)
(9)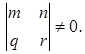 (10)
(10)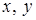 на их выражения через
на их выражения через 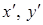 по формулам (9). В новой системе координат уравнение кривой примет вид:
по формулам (9). В новой системе координат уравнение кривой примет вид:

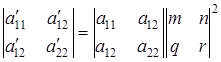 (11)
(11)
 в зависимости от ориентаций ортонормированных базисов этих систем (см. § 9). В этом случае из равенства (19.11) получим:
в зависимости от ориентаций ортонормированных базисов этих систем (см. § 9). В этом случае из равенства (19.11) получим: .
. . Тогда инвариант D имеет вид:
. Тогда инвариант D имеет вид:  . Так как D < 0, то гипербола имеет два асимптотических направления. В этом случае уравнение (7) принимает вид:
. Так как D < 0, то гипербола имеет два асимптотических направления. В этом случае уравнение (7) принимает вид:  . Его корни равны:
. Его корни равны:  . Поэтому векторы асимптотических направлений имеют следующие координаты:
. Поэтому векторы асимптотических направлений имеют следующие координаты:  и
и  , где t - любое действительное число, отличное от нуля. Эти направления параллельны асимптотам гиперболы (см. § 17). Кривые, для которых первый инвариант отрицателен, называются кривыми гиперболического типа. Такие кривые имеют два асимптотических направления.
, где t - любое действительное число, отличное от нуля. Эти направления параллельны асимптотам гиперболы (см. § 17). Кривые, для которых первый инвариант отрицателен, называются кривыми гиперболического типа. Такие кривые имеют два асимптотических направления. и вычислим для нее первый инвариант:
и вычислим для нее первый инвариант:  . Таким образом, парабола имеет одно асимптотическое направление. Для его нахождения составим уравнение (19.7):
. Таким образом, парабола имеет одно асимптотическое направление. Для его нахождения составим уравнение (19.7):  . Координаты векторов асимптотического направления параболы равны: { t; 0}, где t ‑ любое действительное число, отличное от нуля. Эти векторы параллельны оси параболы. Кривые, для которых первый инвариант равен нулю, называются кривыми параболического типа. Такие кривые имеют одно асимптотическое направление.
. Координаты векторов асимптотического направления параболы равны: { t; 0}, где t ‑ любое действительное число, отличное от нуля. Эти векторы параллельны оси параболы. Кривые, для которых первый инвариант равен нулю, называются кривыми параболического типа. Такие кривые имеют одно асимптотическое направление.


