МАТЕМАТИКА. Во 2 младшей гр. - у детей формируются разнообразные практические действия совокупностями однородных и разнородных предметов
МАТЕМАТИКА Методические указания и контрольные задания для студентов-заочников средних специальных учебных заведений
по специальности 270802 «Строительство и эксплуатация зданий и сооружений»
2013 г.
ВАРИАНТ 1
1. Найдите интегралы: 1 2)
2. На тело в горизонтальном направлении действует сила в 30 Н, а в вертикальном – сила 40 Н. Найдите графически равнодействующую силу.
3. Покажите графически и методом алгебраического сложения, что система не имеет решения: 3y – 3x = 2, 5x - 5y = 7.
4. Постройте график функции y = 3x3 –x + 2.
5. В урне находятся 12 шаров, из которых 4 белые, а остальные черные. Найдите: а) вероятность того, что взятый наугад шар является черным; б) вероятность того, что два взятых наугад шара окажутся белыми.
ВАРИАНТ 2
1. Найдите интегралы:
2. На тело вертикально вверх действует сила 5 Н, а вертикально вниз – сила 7 Н. Найдите графически равнодействующую силу.
3. Покажите графически и методом подстановки, что система бесконечное множество решений: 2x + y = 7, y = 7 – 2x.
4. Постройте график функции y = x4 – 8x2 + 16.
5. В партии из 30 деталей имеется 6 бракованных. Найдите: а) вероятность того, что взятая наугад детальокажется бракованной; б) вероятность того, что из двух выбранных наугад деталей ни одна не окажется бракованной.
ВАРИАНТ 3
1. Найдите площадь фигуры, ограниченной заданными линиями: параболойy = 4x - x2, прямой y = 4 – x и осью Ox.
2. Решите систему и проиллюстрируйте решение графически: 4x + 3y = 29, 2x – y = 7.
3. Постройте график функции y = x3 – 6x2 + 9х - 3.
4. Студент из 30 экзаменационных вопросов программы подготовил 25. Билеты содержат по 3 вопроса. Какова вероятность того, что все вопросы, содержащиеся в билете, известны студенту?
5. Геолог проехал 40 км на машине на юго-восток из города А в город В, а затем прошел пешком на запад 25 км из пункта В в пункт С. Найдите графически сумму этих векторов. Измерьте ее длину.
ВАРИАНТ 4
1. Найдите площадь фигуры, ограниченной заданными линиями: параболойy = 4 - x2, прямой y = x + 2 и осью Ox.
2. Решите систему и проиллюстрируйте решение графически: 2х + 5у = 0, -8x+15y = 7.
3. Постройте график функции y =
4. Партия из 50 деталей содержит 4 бракованных. Какова вероятность того, что среди 10 случайно выбранных деталей бракованных нет?
5. Даны векторы
ВАРИАНТ 5
1. Определите скорость тела, движущегося по закону S(t) =
2. Решите систему и проиллюстрируйте решение графически: 5х + у = 7, 3x-2y = 12.
3. Постройте график функции y = -x4+2х2 + 3.
4. Группа их четырех мальчиков и четырех девочек делится случайным образом на две равные группы. Найдите вероятность того, что в кжадой группе число мальчиков и девочек одинаково.
5. Даны векторы
1. Найдите следующие пределы
2. Найдите производную функций:
x - 7 = 3y, y =
4. Постройте график функции y =
5. В урне находятся 10 шаров, из которых 2 белые, а остальные черные. Найдите: а) вероятность того, что взятый наугад шар является черным; б) вероятность того, что три взятых наугад шара окажутся черными.
ВАРИАНТ 7
1. Найдите интервалы монотонности функций:
2. Вычислите:
5x -3y = 26, 2x + y = 17.
4. Группа студентов должна сдавать экзамены по четырем предметам. Сколькими способами можно составить расписание экзаменов?
5. Даны векторы
ВАРИАНТ 8
1. Найдите интегралы:
2. Даны векторы
3. Решите систему уравнений методом Крамера
15x-16y = 24, 3x - 4y = 0.
4. Постройте график функции y = (x + 1)(x + 3).
5. Сколькими способами 7 различных путевок можно распределить в бригаде из 7 рабочих?
ВАРИАНТ 9
1. Найдите наибольшее и наименьшее значения функцииf(x) =
2. Даны векторы
3. Покажите графически и методом подстановки, что система не имеет решения: 2x- 2y = 1, y - x = -1.
4.Найдите следующие пределы
5. Группа из 28 студентов обменялась фотокарточками. Сколько всего было роздано фотокарточек?
ВАРИАНТ 10
1. Составьте уравнение касательной и нормали к графику функции f(x) = x2 + 4x + 5 в точке с абсциссой x0 = -3.
2. Даны векторы
3. Решите систему уравнений методом Крамера 64x + 51y = 90, 25x+34y = 7.
4. Решите уравнения:
5. Вычислите: а)
|


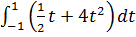
 2dx
2dx
 x3 – х.
x3 – х. .
. в момент времени t = 10.
в момент времени t = 10. .
.

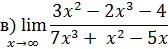



 x3 – x2 + 1.
x3 – x2 + 1.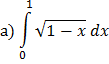


 .
.


 .
. на отрезке [-1;2]
на отрезке [-1;2] .
.
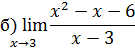

 – 6 = 0
– 6 = 0

 б)
б) 



