Элементы теории вероятностей
Опытом, или испытанием, называют всякое осуществление комплекса условий или действий, при которых наблюдается соответствующее явление. Возможный результат опыта называют событием. Случайным называется событие, которое в данном опыте может произойти, а может и не произойти. Вероятность события А определяется формулой Р(А) = где п — число всех равновозможных элементарных исходов опыта, т — число элементарных исходов, благоприятствующих событию А. Пример. Для проведения лотереи отпечатали 2000 билетов, из которых 100 выигрышных. Какова вероятность того, что билет окажется выигрышным? Решение. Общее число исходов равно количеству лотерейных билетов, то есть n=2000. Благоприятных исходов — купить выигрышный билет m=100. Так как все исходы равновозможные, то вероятность того, что купленный билет окажется выигрышным, равна Случайной называют величину, которая в результате испытания принимает то или иное значение, меняющееся от случая к случаю. Её называют дискретной, если значения можно представить в виде числовой последовательности. Помимо значения дискретная случайная величина (ДСВ) характеризуется вероятностью появления. Соответствие между значениями ДСВ и вероятностью их появления называют законом распределения. Закон распределения ДСВ задается таблицей (Х – случайная величина, Р – вероятность)
События образуют полную группу, тогда обязательное условие:
Числовые характеристики ДСВ: Математическое ожидание Дисперсия Среднее квадратическое отклонение
Пример. Дискретная случайная величина Х имеет закон распределения:
Чему равна вероятность Решение. Из условия Математическое ожидание случайной величины Х:
Составим закон распределения случайной величины Х2
Математическое ожидание случайной величины Х2:
Вычислим дисперсию: Среднее квадратическое отклонение: Ответы: 0,2; 0,6; 0,408; 0,048; 0,22.
|


 =
=  = 0,05. Ответ: 0,05.
= 0,05. Ответ: 0,05.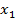

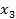


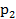

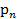


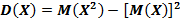


 находим
находим 

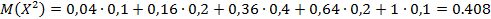
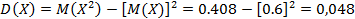
 . Округлили до сотых.
. Округлили до сотых.


