Математический анализ
В данном разделе математики исследуют функции на основе интегрального и дифференциального исчисления. Для изучения скорости изменения функции y=y(x) по отношению к ее агрументу х применяют такое понятие как производная. Обозначается знаком Вычисление производной функции называют дифференцированием.
Некоторые правила дифференцирования: 1) производная суммы функций равна сумме производных от каждой функции; 2) постоянный множитель выносят за знак производной. Формулы производной:
Пример 1. Решение: применяя правило (1) и формулы, получим:
Пример 2. Решение: применяя правила (1, 2) и формулы, получим:
|
(читается «игрек штрих»). Производная функции 
- производная постоянной
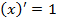
. Вычислить производную 
. Вычислить производную 
