Тематика контрольных работ и РГР
КР №1. Вычисление кратных интегралов -нахождение площади плоской фигуры; -нахождение объема поверхностей; -нахождение длины дуги; - вычисление поверхностных интегралов 1 и 2 рода;
КР №2. Приложения кратных интегралов - вычисление моментов инерции; - нахождение координат центра масс; - поток векторного поля; - дивергенции векторного поля; - ротор векторного поля скоростей; - оператор Гамильтона.
МАТЕМАТИКА ЧАСТЬ 4 Для групп 23177, 23178, 23179 Вопросы к экзамену и тестовые задания Сдавать к.работу не надо, уметь решать задачи такого типа Содержание дисциплины Дифференциальные уравнения первого порядка Уравнения первого порядка и методы их интегрирования. Уравнения в полных дифференциалах и методы их интегрирования. Линейные уравнения и методы их интегрирования. Приближенное решение уравнений первого порядка Дифференциальные уравнения высших порядков Уравнения второго порядка, допускающие понижение порядка. Дифференциальные уравнения высших порядков. Линейные дифференциальные уравнения второго порядка. Линейные неоднородные дифференциальные уравнения второго порядка. Линейные однородные дифференциальные уравнения второго порядка Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Применение линейных дифференциальных уравнений к изучению колебательных явлений Уравнения математической физики Уравнения колебаний. Уравнения теплопроводности. Методы решения уравнений в частных производных. Системы дифференциальных уравнений Методы интегрирования систем дифференциальных уравнений. Основы преобразований Лапласа. Решение дифференциальных уравнений операционным методом. Решение систем дифференциальных уравнений операционным методом
Вопросы к экзамену
20. О вариант теста по дифференциальным уравнениям 1.Дано дифференциальное уравнение
2.Дано дифференциальное уравнение –1 3.Дано дифференциальное уравнение
С D B A 4.Общий интеграл дифференциального уравнения
имеет вид…
5.Дано линейное однородное дифференциальное уравнение
6.Частному решению линейного неоднородного дифференциального
7.Порядок дифференциального уравнения 8.Уравнение уравнение Бернулли однородное дифференциальное уравнение уравнение с разделяющимися переменными линейное неоднородное дифференциальное уравнение I порядка 9.Дано дифференциальное уравнение
|

 .Тогда его решением является функция…
.Тогда его решением является функция…
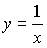


 , тогда функция
, тогда функция  является его решением при k равном…
является его решением при k равном… при
при  . Тогда интегральная кривая, которая определяет решение этого уравнения, имеет вид…
. Тогда интегральная кривая, которая определяет решение этого уравнения, имеет вид…



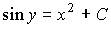
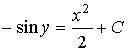
 , тогда его общее решение имеет вид…
, тогда его общее решение имеет вид…



 по виду его правой части соответствует функция …
по виду его правой части соответствует функция …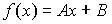
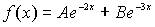


 равен …
равен … является
является . Тогда соответствующее ему характеристическое уравнение имеет вид …
. Тогда соответствующее ему характеристическое уравнение имеет вид …