Решение. 2.1. Построение экономико-математических моделей практических задач
Полковник Н.Карпов
ЛЕКЦИЯ 2. ПРАКТИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ ОСНОВ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ В ВЫБОРЕ ОПТИМАЛЬНОГО УПРАВЛЕНЧЕСКОГО РЕШЕНИЯ 2.1. Построение экономико-математических моделей практических задач 2.2. Решение транспортной задачи методом потенциалов. 2.3. Решение задачи о назначениях.
2.1. Эффективность решения большинства экономических задач зависит от наилучшего способа использования ресурсов (деньги, товары (услуги), сырье, оборудование). В качестве метода оптимизации используется линейное программирование.
Линейное программирование – это математический метод поиска максимума или минимума целевой функции при наличие системы ограничений.
Управленческое решение, которое удовлетворяет условия задания и соответствует цели, называют оптимальным. Оптимизационная задача содержит 2 составляющие: - целевую функцию - систему ограничений
F (х1, х2, х3, х4,….. хn,)→max (min)
bm – заданные постоянные величины Основная процедура формулировки задач линейного программирования состоит из 4 этапов:
1. Определение переменных задачи, значения которых нужно получить в пределах существующих ограничений. 2. Определение цели и ограничений на ресурсы. 3. Описание цели через переменные задачи. 4. Описание ограничений через переменные задачи
Пример 1(Производственная задача)
Предприятие может выпускать три вида продукции – А. В. С. Производственные возможности предприятия характеризуются следующими данными: а) суточный фонд рабочего времени оборудования – 800 часов; б) суточный расход сырья – 850 т; в) суточный расход электроэнергии – 600 кВт - часов Известны нормы затрат ресурсов на единицу продукции каждого вида и оптовые цены. Постройте экономико-математическую модель задачи, обеспечивающую максимальный доход от реализации продукции. Таблица 1
Решение
1. Обозначим через хj количество единиц продукции j-го вида, запланированных к производству.
х1 - продукции А х2- - продукии В х3- продукции С
2. Цель - максимизация дохода от реализации продукции, объем производства ограничен количеством (оборудования, сырья, электроэнергии) и максимальным прогнозным спросом на продукцию. 3. F (x)= 10х1+9х2 + 8х3 → max
Пример 2. Предполагается к реализации 4 инвестиционных проектов Р1, Р2, Р3, Р4
Экономические оценки ожидаемого эффекта от их реализации составляют Сj Необходимая величина капиталовложений - g. Общий объем возможных инвестиций ограничен величиною G.
Как распорядится имеющимися финансовыми ресурсами, чтобы максимизировать суммарных эффект от инвестиций? (составить экономико-математическую модель задачи).
Решение 1. Введем логическую переменную хj ={1, если Рj – принять, 0, если отклонить
2. Цель - максимизировать суммарных эффект от инвестиций, Общий объем возможных инвестиций ограничен 60 млн.грн. 3. F (x)= 48х1+55х2 + 45х3 +39х4 → max
4.
2.2.
В транспортной задаче (Т –задаче) необходимо составить оптимальный план, т.е. найти такие значения объема перевозок грузов хij от поставщиков Аi к потребителям В j, чтобы:
1- вывести все грузы от поставщиков 2 – удовлетворить заявки каждого потребителя 3 – обеспечить минимальные транспортные расходы Сij на перевозку грузов.
Все исходные данные Т- задачи можно записать в виде таблицы.
Целевая функция Т-задачи:
Условие, необходимое для разрешимости Т-задачи, сводиться к балансу: Σ ai = Σ bi . Такие задачи называются закрытыми (в противном случае называются открытыми).
Для нахождения первоначального базисного распределения поставок используют метод «минимальной стоимости». Алгоритм метода рассмотрим на примере.
Пример. На три базы P, Q, R поступил однородный груз в количествах 9,4 и 8 единиц. Этот груз требуется перевезти в три магазина А,В,С в количествах 3,5 и 6 единиц. Составьте оптимальный план транспортировки грузов, так чтобы общая стоимость транспортировки была минимальной. Стоимость транспортировки единицы груза приведены в табл.
1. Проверим сбалансированность транспортной задачи, для этого необходимо чтобы
Σ ai =9+4+8=21 Σ bi =3+5+6=14 (открытый тип задачи) Поэтому вводим «фиктивный»магазин, его потребность будет равна 21-14=7 изделий и предполагается, что затраты транспортировки равны 0.
2. Применим метод «минимальной стоимости». - в клетку с минимальной стоимостью записываем наибольшее возможное количество продукта. -производится корректировка оставшихся объемов предложения и потребностей. - выбирается следующая стоимость, в которую помещается наибольшее возможное количество продукта, и.т.д.
Количество перевозок должно быть равно m+n –1 =4+3–1=6
Целевая функция первоначального плана:
3. Одним из методов проверки первоначального плана на оптимальность – является метод потенциалов. Потенциалами называется система чисел, приписанных соответственно каждой строке i и каждому столбцу j.
Экономическая сущность потенциалов: потенциал Ui можно принять условно за цену товару в пункте его производства, потенциалом Vj можно принять условно за цену товару в пункте его потребления.
Vj = Ui + Сij
Строим систему потенциалов. Начинаем с того, что строке 1 присваиваем потенциал U1=0.
Проверка на оптимальность: Для свободных квадратов должно выполняться условие:
Ui + Сij ≥ Vj
U1 + С11 ≥ V1 0+10≥-1 U1 + С12 ≥ V2 0+20≥18
U2 + С21 ≥ V1 8+2≥-1 U2 + С23 ≥ V3 8+8≥5 U2 + С24 ≥ V4 8+0≥0 U3 + С34 ≥ V4 -2+0≥0 (условие не выполняется, план не оптимальный).
Для оптимизации плана необходимо переместить перевозку в квадрант 3.4. Перемещение производиться таким образом, чтобы по отношению к выбранному квадранту образовать связку. Для этого необходимо провести замкнутую ломаную линию, в которой одной из вершин многоугольника является свободный квадрат, а остальные вершины находятся в занятых квадратах. Затем присваиваем знаки «+» и «–» начиная со свободного квадрата. Из квадратов со знаком «–» перемещаем перевозки в квадраты со знаком «+». Перемещается наименьшее количество, которое находится в квадратах связки со знаком «–».
–
+
– + перемещаем число «4»
Строим новую систему потенциалов и проверяем план на оптимальность.
Для всех свободных квадратов выполняться условие: Ui + Сij ≥ Vj, поэтому план оптимальный.
Целевая функция оптимального плана:
Ответ: 6 изделий перевозятся с базы P в магазин С., 3 изделия остаются на базе P., 4 изделия перевозятся с базы Q в магазин В, с базы R перевозятся 3 изделия в магазин А, 1 изделие в магазин В, 4 изделия остаются на базе R.
2.3. Частным случаем Т-задачи является задача о назначениях, в которой в каждом пункте назначения объем производства равен 1, и величина предложения каждого пункта производства равна 1.
Пример: Компания имеет 4 сбытовые базы и 4 заказа, которые необходимо доставить различным потребителям. Складские помещения каждой базы достаточны чтобы вместить один из этих заказов. Дано расстояние между базой и каждым потребителем. Распределите заказы по базам, чтобы общая дальность транспортировки была минимальной.
Исходные данные
Мат.модель задачи:
1. Введем логическую переменную хj ={1, если назначить, 0, если не назначить
2. Цель – минимизация общей дальности транспортировки. 3. F (x)= 68х1+73х2 + 75х3 +83х4 +56 х5 +61 х6 +58 х7 +63 х8 +38 х9 +………..+45 х16→ min
4.
Табличный алгоритм решения задачи:
1. В каждой строке таблицы найти наименьший элемент и вычесть его из всех элементов данной строки. 2. Повторить то же самое для столбцов. 3. Найти строку, содержащую только одно нулевое значение стоимости и в данную клетку поместить одно назначение. Зачеркнуть оставшиеся нулевые значения столбцов. 4. Найти столбец, содержащий только одно нулевое значение стоимости и в данную клетку поместить одно назначение. Зачеркнуть оставшиеся нулевые значения в строках. 5. Если план не оптимальный, то провести минимальное количество прямых через строки и столбцы матрицы (но не по диагонали) таким образом, чтобы они проходили через все нулевые значения. 6. Найти наименьший среди элементов, через которые не проходят прямые. Прибавить найденный элемент ко всем элементам, которые лежат на пересечении проведенных прямых. Все элементы, через которые проходит только одна прямая, оставить без изменения.
Решение
1 этап 2 этап.
.
3,4 этапы:
- план не оптимальний: на первом этапе оптимизации – 3 назначения:
5 этап.:
6 этап: min элемент =_____
Ответ: F(x)= = 208 км.
|



 4.
4. 


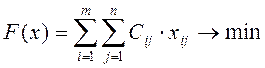



 Ui
Ui
 2
2







