Помимо частот (или наблюдаемых величин) SPSS может вычислять ожидаемые значения для каждой ячейки таблицы. Ожидаемое значение вычисляется в предположении, что две номинативные переменные независимы друг от друга. Рассмотрим простой пример. Пусть в комнате находится 100 человек, из которых 30 являются мужчинами, а 70 - женщинами. Если известно, что из этих 100 человек 10 увлекаются искусством, то в случае, если увлечение не зависит от пола, мы будем ожидать, что из 10 увлекающихся искусством 3 являются мужчинами, а 7 - женщинами. Сопоставляя эти ожидаемые частоты с наблюдаемыми частотами, мы можем судить о том, действительно ли два номинативных признака не связаны. Чем больше расхождение наблюдаемых и ожидаемых частот, тем, очевидно, два признака сильнее связаны друг с другом. Целью применения критерия независимости  и является установление степени соответствия между наблюдаемыми и ожидаемыми значениями ячеек.
и является установление степени соответствия между наблюдаемыми и ожидаемыми значениями ячеек.
В основе критерия независимости лежит вычисление величины  определяемой как сумма отношений суммы квадратов отклонений наблюдаемой величины
определяемой как сумма отношений суммы квадратов отклонений наблюдаемой величины 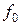 от ожидаемой величины
от ожидаемой величины  . к ожидаемой величине каждой ячейки:
. к ожидаемой величине каждой ячейки:

Как можно видеть из формулы, при больших отклонениях 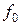 от
от  величина
величина  также становится большой. Вместе с
также становится большой. Вместе с  вычисляется р -уровень значимости. При р > 0,05 считается, что различия между наблюдаемыми и ожидаемыми значениями незначительны. В противном случае предположение о независимости двух номинативных переменных отклоняется и делается вывод о том, что две классификации (переменные) зависят друг от друга. Более подробные описания величии, связанных с критерием
вычисляется р -уровень значимости. При р > 0,05 считается, что различия между наблюдаемыми и ожидаемыми значениями незначительны. В противном случае предположение о независимости двух номинативных переменных отклоняется и делается вывод о том, что две классификации (переменные) зависят друг от друга. Более подробные описания величии, связанных с критерием  , вы можете найти в разделе «Представление результатов» этой главы.
, вы можете найти в разделе «Представление результатов» этой главы.
Зачастую величина  ошибочно воспринимается исследователями как величина силы связи между переменными. Однако это не так, поскольку
ошибочно воспринимается исследователями как величина силы связи между переменными. Однако это не так, поскольку  в значительной степени определяется числом переменных таблицы сопряженности и размером выборки. Таким образом, сравнение двух значений
в значительной степени определяется числом переменных таблицы сопряженности и размером выборки. Таким образом, сравнение двух значений  , полученных при разных условиях, становится бессмысленным. По этой причине Пирсон (Pearson) предложил коэффициент «фи», получаемый извлечением квадратного корня из отношения
, полученных при разных условиях, становится бессмысленным. По этой причине Пирсон (Pearson) предложил коэффициент «фи», получаемый извлечением квадратного корня из отношения  к размеру выборки N. Целью введения новой величины было получения наглядной интерпретации связи между переменными в виде коэффициента, лежащего в пределах от 0 до 1 и принимающего нулевое значение для независимых переменных и единичное значение для строго связанных переменных. Однако цель не была достигнута полностью: если одна из переменных таблицы сопряженности имеет более двух градаций, значение «фи» может превышать 1. Крамеру (Cramer) удалось исправить последний недостаток путем введения коэффициента V. Этот коэффициент всегда принимает значения от 0 до 1 и служит характеристикой силы связи между переменными.
к размеру выборки N. Целью введения новой величины было получения наглядной интерпретации связи между переменными в виде коэффициента, лежащего в пределах от 0 до 1 и принимающего нулевое значение для независимых переменных и единичное значение для строго связанных переменных. Однако цель не была достигнута полностью: если одна из переменных таблицы сопряженности имеет более двух градаций, значение «фи» может превышать 1. Крамеру (Cramer) удалось исправить последний недостаток путем введения коэффициента V. Этот коэффициент всегда принимает значения от 0 до 1 и служит характеристикой силы связи между переменными.

 и является установление степени соответствия между наблюдаемыми и ожидаемыми значениями ячеек.
и является установление степени соответствия между наблюдаемыми и ожидаемыми значениями ячеек.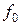 от ожидаемой величины
от ожидаемой величины  . к ожидаемой величине каждой ячейки:
. к ожидаемой величине каждой ячейки:



