Методы самоконтроля

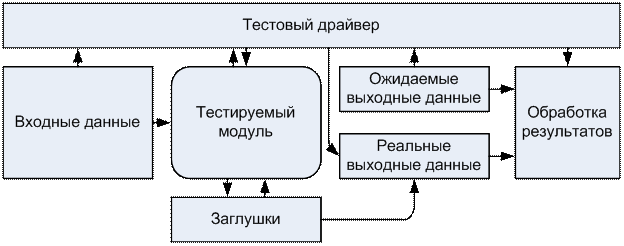
Основной объем тестирования практически любой сложной системы обычно выполняется в автоматическом режиме. Кроме того, тестируемая система обычно разбивается на отдельные модули, каждый из которых тестируется вначале отдельно от других, затем в комплексе.

Это означает, что для выполнения тестирования необходимо создать некоторую среду, которая обеспечит запуск и выполнение тестируемого модуля, передаст ему входные данные, соберет реальные выходные данные, полученные в результате работы системы на заданных входных данных. После этого среда должна сравнить реальные выходные данные с ожидаемыми и на основании данного сравнения сделать вывод о соответствии поведения модуля заданному (Рис. 2).

 

Рис. 2 Обобщенная схема среды тестирования

Тестовое окружение также может использоваться для отчуждения отдельных модулей системы от всей системы. Разделение модулей системы на ранних этапах тестирования позволяет более точно локализовать проблемы, возникающие в их программном коде. Для поддержки работы модуля в отрыве от системы тестовое окружение должно моделировать поведение всех модулей, к функциям или данным которых обращается тестируемый модуль.

Поскольку тестовое окружение само является программой (причем, часто не на том языке программирования, на котором написана система), оно само должно быть протестировано. Целью тестирования тестового окружения является доказательство того, что тестовое окружение никаким образом не искажает выполнение тестируемого модуля и адекватно моделирует поведение системы.

 

ВЕРИФИКАЦИЯ

Методы самоконтроля

1. Прикидки. В процессе применения математики к решению реальной задачи выдача результата обычно связана с определенной моральной и/или материальной ответственностью. Поэтому на всех стадиях исследования с целью предотвращения ошибок широко применяются различные методы самоконтроля.

Большую пользу приносят разного рода прикидки, которые могут быть направлены как на получение предварительных сведений о самом решении, так и на упрощение уравнений задачи — что, впрочем, взаимосвязано. Для первого полезно неформальное обсуждение условий задачи, по возможности ясное представление картины изучаемого процесса, привлечение интуиции, аналогий с ранее изученными случаями и т. п. Эту прикидку можно получить и с помощью максимально возможного упрощения геометрических форм и уравнений задачи. Знание, хотя бы самое грубое, качественных и количественных характеристик искомого решения может помочь при выборе более точного метода.

Сравнение свойств решения, полученного более точными методами, с предварительными сведениями о нем дает дополнительное средство контроля, так как соответствие этих данных значительно повышает доверие к результатам. Существенное рассогласование между этими данными свидетельствует об ошибочности либо одних, либо других (а может быть, и тех и других); в этом случае нужны проверка и обсуждение всех данных. Такое обсуждение полезно и для развития интуиции в области, к которой относится решаемая задача.

С помощью прикидок мы можем получить характерные значения участвующих величин и перейти к безразмерной форме уравнений задачи. Это дает возможность прикинуть величину отдельных членов уравнения и сравнительно малые члены либо отбросить, либо упростить, либо учесть с помощью метода малого параметра. После решения упрощенного таким образом уравнения можно путем подстановки проверить, в самом ли деле относительно малы отброшенные члены. Прикидки систематически проводятся и для текущего контроля вычисления арифметических и более сложных выражений, интегралов и т. п., особенно в случаях, когда есть опасность ошибиться в порядке величины (неправильно написать показатель степени у десятки).

2. Контроль размерностей. Этот простой, но важный тест состоит из трех правил:

1) складывать друг с другом и связывать неравенствами можно только величины одинаковой размерности;

2) если размерность какой-либо величины, представленной некоторой формулой, известна заранее, то эта размерность должна вытекать и из данной формулы;

3) аргумент неалгебраической функции должен быть безразмерным, т. е. числом (в частности, безразмерным должен быть и аргумент тригонометрических функций в соответствии с правилом: sin (угла в х радиан) = sin (числа x)).

Так как ошибку желательно обнаружить по возможности раньше, описанную проверку следует проводить не только по окончании вывода того или иного соотношения, но и на промежуточных стадиях этого вывода.

Для безразмерных величин правила контроля размерностей не действуют. Стремление к контролю размерностей приводит к тому, что если в формулировке задачи даны конкретные значения параметров, то часто оказывается удобным обозначить эти значения буквами, считая их размерными, затем решить задачу в буквенном виде и лишь после этого подставить вместо букв их значения. При переходе к действиям с числами здесь добавляется контроль системы единиц, согласно которому все величины должны быть выражены в одной и той же системе единиц.

3. Другие виды контроля. Перечислим еще некоторые (не все!) применяемые методы контроля.

Контроль законов сохранения. Если в содержательной модели потери энергии или массы считались пренебрежимо малыми, то математическая модель должна удовлетворять условию сохранения энергии или массы, а потому и для решений должно проявляться это свойство.

Контроль характера зависимости решения от параметров задачи. Здесь речь идет о проверке направления, а иногда и скорости изменения найденной величины при изменении параметров задачи: эти направления, вытекающие из выведенных соотношений, должны быть такими, как следует непосредственно из смысла задачи.

Контроль экстремальных ситуаций. Всегда оказывается чрезвычайно полезным проследить за тем, какой вид принимают как исходные, так и промежуточные и окончательные соотношения, а также выводы из исследования модели, если ее параметры приближаются к крайним допустимым для них значениям — чаще всего к нулю или к бесконечности. В таких экстремальных ситуациях задача часто упрощается или вырождается, так что соотношения приобретают более наглядный смысл и могут быть проверены — если, как это часто бывает, соответствующие им решения можно получить независимо от анализа общего случая или если они заранее известны.

Контроль математической замкнутости состоит в проверке того, что выписанные математические соотношения дают возможность решить поставленную математическую задачу, т. е. что математическая модель полна. Так, если задача свелась к отысканию неизвестных величин с помощью решения системы конечных уравнений, то надо проверить, что этих уравнений столько же, сколько неизвестных.

Если задача свелась к отысканию конкретного решения дифференциального уравнения, то надо проверить, что поставлены также добавочные (начальные, граничные) условия, определяющие это решение.

Упомянем еще о таком способе проверки правильности окончательного или промежуточного результата: если сложным, обходным путем получена простая формула, то пытаются найти более прямой путь ее вывода, что дает возможность не только подтвердить ее справедливость, но и глубже ее понять.

4. Роль примеров. Для успешного исследования математической модели и избегания ошибок особенно велика роль правильной интуиции, ориентировки в рассматриваемом круге вопросов. А для этого, в свою очередь, весьма полезным оказывается подробный разбор примеров, частных случаев, элементов модели. С помощью таких примеров можно выбирать и отрабатывать методы исследования математической модели, формулировать и проверять те или иные гипотезы. Каждый пример служит как бы моделью интересующей нас более общей или более сложной модели, он выявляет некоторые свойства последней и способствует их пониманию.

Существенно, что примеры часто удается исследовать значительно детальнее и с более высокой достоверностью, чем общую модель.

5. О верификации модели. Проблема верификации модели, т. е. выяснения ее адекватности, значительно выходит за рамки самоконтроля, но о ней нельзя упомянуть. Действительно ли, составляя уравнения и выбирая исходные данные, мы правильно учли все существенные для нас факторы, причем с необходимой точностью? Ответ на этот вопрос имеет кардинальное значение для проводимого исследования или расчета. Если речь идет о модели, достаточно апробированной в рассматриваемой области приложений, то вопрос о верификации обычно не возникает, мы полностью полагаемся на предшественников. Он становится существенным, если мы строим модель заново, применяя известные ранее приемы, либо применяем известную модель вне рамок, в которых она показала себя адекватной, либо, наконец, строим принципиально новую модель. Во всех этих случаях, особенно в двух последних подтверждение адекватности модели весьма желательно, без этого такая адекватность остается лишь более или менее правдоподобной гипотезой.

Основным подтверждением адекватности принятой модели является согласие следствий из нее с известными из эксперимента или из независимых теоретических исследований свойствами моделируемого объекта. При этом, чем больше окажется таких независимых подтверждений, тем большее доверие приобретает модель.

Так, например, нас может интересовать форма нормальных (т. е. гармонических или затухающих гармонических) колебаний системы, но из эксперимента нам известны только их частоты; тогда совпадение рассчитанных частот с экспериментальными может служить подтверждением правильности расчета форм.

Правильность модели может подтверждаться и предсказанием с ее помощью какого-либо эффекта, относящегося к известному прошлому. Порой бывает и так: мы с помощью модели получаем только те результаты, которые нам уже известны из опыта. При этом модель подтверждается как бы впрок, в расчете на дальнейшие применения в условиях, не охваченных экспериментом. К тому же математический анализ свойств объекта часто приводит к их более глубокому пониманию, что полезно само по себе.

Отметим еще следующее важное обстоятельство: при теоретическом подтверждении модели надо следить за независимостью подтверждающих соображений от подтверждаемых.

Если обнаружено существенное расхождение между рассчитанными и известными свойствами, то модель необходимо изменить. Это можно делать, либо привлекая дополнительные теоретические соображения, либо путем подгонки, либо с помощью комбинации того и другого.