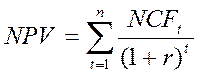Классический подход.
Наиболее часто используемым критерием принятия решения относительно проекта является параметр чистой приведенной стоимости денежных потоков проекта — NPV. Чистая приведенная стоимость фактически представляет собой расчет суммы приведенных к сегодняшнему эквиваленту суммы чистых денежных потоков проекта при ставке дисконтирования, равной прибыльности альтернативных проектов с аналогичным уровнем риска. Подсчет можно произвести по формуле:
NCFt — величина чистого денежного потока проекта; r — норма дисконтирования; t — временная отдаленность денежного потока от изначальной точки. Достаточно распространенной в практике функционирования отечественных предприятий является ситуация, когда, проведя обоснование проекта и рассчитав единственное значение NPV, принимают решение. В противовес данному подходу анализ чувствительности предусматривает проведение следующих процедур: 1. Формируют модель обоснования проекта в виде набора бюджетов, используя MS Excel, Project Expert либо другое специализированное программное обеспечение. 2. Рассматривают такую модель как черный ящик, систему, на вход которой подаются исходные данные проекта (например, цена продукта, объем предполагаемых продаж, процентная ставка дисконтирования, ставка по кредитам, предполагаемый уровень инфляции и т. д.), на выходе черного ящика «снимают» только один параметр. Чаще всего им служит значение NPV, которое генерирует проект с такими исходными данными. 3. Несколько раз рассчитывают обоснование проекта, пользуясь сформированной моделью при различных значениях исходных данных. При этом набор исходных данных формируют следующим образом: все параметры исходных данных, кроме одного, оставляют постоянными без изменений, а один параметр считают переменным, генерируя сразу несколько его значений (обычно пять) с определенным шагом относительных изменений. Изменения, например, могут составлять –20%; –10%; 0%; +10%; +20%. Модель рассчитывают несколько раз при различных изменениях переменного параметра. Так, если в базовом варианте обоснования предполагалась цена продукта на уровне 50 усл.ед. и именно цена является на данном этапе переменным параметром, то вычисляют, какие значения чистой приведенной стоимости давал бы проект в случае, если цена будет составлять соответственно 40 усл.ед., 45 усл.ед., 50 усл.ед., 55 усл.ед., 60 усл.ед. То есть при приведенном выше относительном приросте переменного параметра по отношению к базовому варианту. 4. Вычисляют относительные темпы прироста полученных значений чистой приведенной стоимости по отношению к NPV базового варианта: (NPV+20%: NPV0% – 1)100%; (NPV+10%: NPV0% – 1)100%; (NPV0%: NPV0% – 1)100%; (NPV–10%: NPV0% – 1)100%; (NPV–20%: NPV0% – 1)100%. 5. Сопоставляют полученные значения удельного прироста NPV с удельным приростом переменного параметра. 6. Процедуру, изложенную в пунктах 3–5, повторяют для других исходных параметров, приняв в качестве переменных каждый из них по отдельности и зафиксировав другие. Результаты проведенного анализа часто принято представлять в виде графика, получившего название паукообразной диаграммы (spider diagram). Очевидно, что всего предусмотреть невозможно, но именно те параметры, удельное изменение которых вызывает наибольшее удельное изменение чистой приведенной стоимости, предусмотреть можно. Именно они являются факторами наибольшего риска по проекту. Соответственно менеджеры в процессе внедрения проекта именно этим факторам должны уделять наибольшее внимание. Целесообразно также создать и реализовать план мероприятий по контролю данных факторов в процессе внедрения проекта. В процессе практической реализации анализа чувствительности с целью минимизации усилий на его реализацию следует учесть ряд практических моментов, скорее, из области информационных технологий: 1. при построении исходной модели проекта следует придерживаться принципа единого введения исходных данных; 2. все параметры проекта должны рассматриваться как такие исходные данные; 3. нужно всегда иметь резервную копию базовой модели в отдельном файле; 4. необходимо оставлять подробную инструкцию и описание модели. Одним из недостатков анализа чувствительности является предпосылка того, что каждый исходный параметр изменяется, независимо от других. Исправить подобную ситуацию помогает анализ сценариев, когда изменяется сразу группа взаимозависящих показателей. Например, следуя классическому закону спроса и предложения, мы можем установить взаимосвязь между параметрами цены и объема продаж. Количество и взаимосвязи исходных параметров модели могут представлять собой достаточно сложную систему. В этом случае имеет смысл отдельно рассматривать развитие событий, соответствующее оптимистическому, ожидаемому и пессимистическому варианту развития. Для каждого из вышеуказанных сценариев рассчитываются свои варианты чистой приведенной стоимости проекта, внутренней нормы рентабельности и других показателей.
2.2. Предугадывая развитие событий Еще более сложным вариантом анализа риска проекта является имитационное моделирование. В этом случае мы не просто пробуем предугадать развитие событий, мы пробуем предугадать природу поведения самих исходных данных. Ни для кого не секрет, что большинство из них подчиняются закону нормального распределения Гаусса с присущей им асимметрией и эксцессом. Эти параметры используют в имитационном моделировании, алгоритм которого может быть представлен в виде изложенной ниже последовательности шагов: 1. Как и в предыдущем случае, формируем модель обоснования проекта в виде набора бюджетов, используя Project Expert либо другое специализированное программное обеспечение. 2. Аналогично соответствующему шагу в алгоритме анализа чувствительности при имитационном моделировании также рассматриваем такую модель как черный ящик, систему, на вход которой подаются исходные данные проекта (например, цена продукта, объем предполагаемых продаж, процентная ставка дисконтирования, ставка по кредитам, предполагаемый уровень инфляции и т. д.). На выходе черного ящика «снимаем» только один параметр. Чаще всего им служит значение NPV, которое генерирует проект с такими исходными данными. 3. Выбираем переменный параметр и при необходимости фиксируем остальные, но в отличие от предыдущего метода расчеты половины модели ведем следующим образом. «Бомбардируем» модель случайными числами с законом распределения, характерным для поведения исходного переменного параметра при остальных зафиксированных значениях. Серии случайных чисел могут составлять последовательности, состоящие из нескольких тысяч и даже десятков тысяч значений, имитирующих изменение переменного параметра, в то время как при проведении анализа чувствительности такая серия состояла только из пяти значений. 4. Обрабатываем полученные значения результирующего параметра (например, значения чистой приведенной стоимости) для того, чтобы определить характеристики поведения результирующей величины. Определяем асимметрию и эксцесс результирующего параметра. 5. Сопоставляем соответствующие законы поведения исходных параметров с законом поведения результирующей величины. Изменения в параметрах распределения результирующего параметра по отношению к параметрам поведения исходного фактора будут указывать на значимость, уровень риска и тенденцию к изменению результирующего параметра проекта. 6. Делаем соответствующие выводы и составляем план управления факторами риска. Следует отметить, что в целом данный метод является достаточно трудоемким, ведь он предусматривает циклическое повторенные одних и тех же вычислений по модели много тысяч раз в процессе подстановки в качестве исходных данных серии случайных чисел, из-за которых метод получил второе название метода Монте-Карло. В этом случае на помощь менеджерам приходит специализированное программное обеспечение, например Project Expert, продукты MS Office.
III. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ В ВЕК КОМПЬЮТЕРОВ. Основные черты современного математического моделирования связаны с тем, что в последнее десятилетие оно быстро теряет академические черты чисто научного и узкопрофессионального направления. Это относится не только к теоретическим вопросам, таким, например, как типизация математических моделей (феноменологические модели, системные модели и все более набирающие силу виртуальные модели) или как проблема адекватности моделей, понимаемая в самом широком смысле. Не менее важны многочисленные проблемы, возникающие при практическом использовании методов и результатов моделирования. В отличие от академической трактовки моделирования (например, как области вычислительной математики), в практике модельных задач большое внимание приходится уделять проблеме взаимоотношения моделирования с «Внешним миром». «Внешний мир» - источник идей и данных для моделирования, в нем живут как заказчики конкретных исследований, так и «Конечные потребители» компьютерной продукции. Поэтому в область моделирования вторгаются проблемы, никак не укладывающиеся в академические рамки, в том числе и разные аспекты общения с «Заказчиком» модели - лицом, для которого и в интересах которого создается модель. Процесс математического моделирования, в общих чертах, можно представить триадой: «модель - алгоритм – программа». Под моделью при этом понимается «эквивалент» объекта, отражающий в математической форме важнейшие его свойства - законы, которым он подчиняется, связи, присущие составляющим его частям, и т.д. Выбор вычислительных алгоритмов - следующий этап, а разработка программ, переводящих модель и алгоритм на понятный компьютеру язык, завершает создание рабочего инструмента исследователя. Готовая триада тестируется в «пробных» экспериментах. На этом этапе посредством цепочки усложнений (иерархии все более полных моделей) обеспечивается ее адекватность. После этого можно переходить к «опытам», дающим все требуемые качественные и количественные свойства и характеристики объекта. Построение моделей представляет собой применение фундаментальных законов природы, вариационных принципов, аналогий, иерархических цепочек. Процесс построения модели включает в себя следующие этапы: 1. Cловесно-смысловое описание объекта или явления (формулировка «предмодели»); 2. Завершение идеализации объекта и упрощение описания; 3. Переход к выбору или формулировке закона (вариационного принципа, аналогии и т.п.) и его записи в математической форме; 4. Завершает формулировку модели ее «оснащение» (задание начального состояния и параметров объекта), формулируется цель исследования. Модель изучается всеми доступными методами (в том числе с применением различных подходов и вычислительных методов); В результате исследования модели достигается поставленная цель. При этом должна быть установлена всеми возможными способами (сравнением с практикой, сопоставлением с другими подходами) ее адекватность - соответствие объекту и сформулированным предположениям.
|