Пусть функция 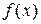 задана в виде табл. 1.
задана в виде табл. 1.
Таблица 1
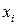 - аргумент функции;
- аргумент функции;
 - значение функции.
- значение функции.
Нужно найти многочлен степени  , чтобы среднеквадратическое уклонение найденных значений от заданных было минимальным, т.е. чтобы соблюдалось соотношение:
, чтобы среднеквадратическое уклонение найденных значений от заданных было минимальным, т.е. чтобы соблюдалось соотношение:
 (1)
(1)
Искомый многочлен имеет вид:
 (2)
(2)
Степень многочлена m задается. Задача нахождения приближающего многочлена  сводится к определению таких его коэффициентов
сводится к определению таких его коэффициентов  , чтобы значение среднеквадратического уклонения
, чтобы значение среднеквадратического уклонения  для этого многочлена было минимальным. Для решения задачи будем использовать необходимое условие экстремума функции
для этого многочлена было минимальным. Для решения задачи будем использовать необходимое условие экстремума функции 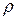 . Найдем экстремум функции, аргументами которой являются
. Найдем экстремум функции, аргументами которой являются  .
.
Для определения экстремума функции (m+1)-го аргумента необходимо приравнять к нулю частные производные этой функции:
 (3)
(3)
После преобразования системы линейных уравнений (3) получим
 (4)
(4)
где
 (5)
(5)
Система уравнений (4) называется нормальной системой метода наименьших квадратов. Решив эту систему относительно  , находим коэффициенты искомого многочлена. Количество уравнений в системе и количество искомых коэффициентов (переменных системы) определяется степенью искомого многочлена приближения. После вычисления коэффициентов многочлена необходимо вычислить величину среднеквадратического уклонения
, находим коэффициенты искомого многочлена. Количество уравнений в системе и количество искомых коэффициентов (переменных системы) определяется степенью искомого многочлена приближения. После вычисления коэффициентов многочлена необходимо вычислить величину среднеквадратического уклонения 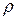 по формуле (1).
по формуле (1).
Значение 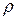 поможет оценить степень приближения многочленном заданной табличной функции. Если значение среднеквадратического уклонения не соответствует заранее заданному, порядок приближающего многочлена необходимо повысить, то есть необходимо увеличить количество переменных и количество уравнений в системе (4). Например, для многочлена первой степени система уравнений (4) примет вид двух уравнений
поможет оценить степень приближения многочленном заданной табличной функции. Если значение среднеквадратического уклонения не соответствует заранее заданному, порядок приближающего многочлена необходимо повысить, то есть необходимо увеличить количество переменных и количество уравнений в системе (4). Например, для многочлена первой степени система уравнений (4) примет вид двух уравнений

а для многочлена второго порядка система уравнений примет вид:

Рассмотрим алгоритм приближения функции многочленом по методу наименьших квадратов в Mathcad на следующем примере.
Пример. Пусть функция  задана таблицей:
задана таблицей:
| x
| 1.50
| 1.51
| 1.52
| 1.53
| 1.54
| 1.55
| 1.56
| 1.57
| 1.58
| 1.59
| 1.60
|
| y(x)
| 0.51183
| 0.50624
| 0.50064
| 0.49503
| 0.48940
| 0.48376
| 0.47811
| 0.47245
| 0.46678
| 0.46110
| 0.45540
|
Методом наименьших квадратов приблизить табличную функцию  многочленами первого, второго, третьего и четвертого порядков. Посчитать величину среднеквадратического уклонения для каждого найденного многочлена. Определить порядок многочлена, дающего наиболее точное приближение. Решение представить графически.
многочленами первого, второго, третьего и четвертого порядков. Посчитать величину среднеквадратического уклонения для каждого найденного многочлена. Определить порядок многочлена, дающего наиболее точное приближение. Решение представить графически.
Прежде чем решать поставленную задачу методом наименьших квадратов, выполним следующие операции по настройке пакета Mathcad и определению исходных данных для задачи. Для этого необходимо:
· Изменить формат чисел так, чтобы в результате вычислений отражалось 5 знаков после десятичной точки.
· Задать степень искомого полинома m. Определить ранжированные переменные i и k, изменяющиеся от 0 до значения степени искомого полинома m. Зададим m=1, в этом случае будем искать приближающий полином первой степени. Ранжированные переменные S и T в нормальной системе (4).
· Создать два вектора 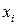 и
и  для ввода значений исходной таблицы.
для ввода значений исходной таблицы.
1. Введем  ;
;
2. Используя палитру векторов и матриц (Vector and Matrix Palette) или сочетание клавиш (Ctrl-M), вызовем оператор матриц и векторов. Появится диалоговое окно Insert Matrix (Вставить матрицу) (рис. 6). В окошко Rows вставить число, равное количеству элементов в векторе – 11. В окошко Columns вставить 1, так как в векторе один столбец. Заполнив окошки, щелкнем по клавише OK, чтобы закрыть его. Появится оператор вектора с полями для ввода данных в виде черных прямоугольников. Заполнить эти поля значениями 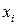 из исходной таблицы.
из исходной таблицы.
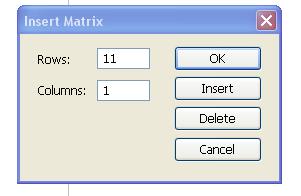
Рис.6. Окно «Вставить матрицу»
· Аналогично создать вектор  и заполнить соответствующими значениями той же таблицы.
и заполнить соответствующими значениями той же таблицы.
Для решения поставленной задачи методом наименьших квадратов введем следующие формулы.
· Формулы нормальной системы метода наименьших квадратов (5). Введем  . Для определения нижних индексов воспользуемся клавишей ([). Для ввода оператора суммирования воспользуемся палитрой вычислений (Calculus Palette) или комбинацией клавиш (Ctrl+Shift+4). Появится оператор суммирования с четырьмя полями для ввода данных. Вставим в поле ввода справа от знака суммы
. Для определения нижних индексов воспользуемся клавишей ([). Для ввода оператора суммирования воспользуемся палитрой вычислений (Calculus Palette) или комбинацией клавиш (Ctrl+Shift+4). Появится оператор суммирования с четырьмя полями для ввода данных. Вставим в поле ввода справа от знака суммы 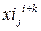 , так как необходимо суммировать вектора
, так как необходимо суммировать вектора  в степени
в степени  . В левое поле под знаком суммы введем индекс суммирования j, а в правое – начальное значение этого индекса, равное 0. Суммирование производится по количеству элементов вектора
. В левое поле под знаком суммы введем индекс суммирования j, а в правое – начальное значение этого индекса, равное 0. Суммирование производится по количеству элементов вектора  , а начинается оно с нуля, так как нумерация элементов вектора в Mathcad по умолчанию начинается с нуля. В поле над знаком суммы вставим конечное значение индекса суммирования: 10 (по количеству элементов в векторе
, а начинается оно с нуля, так как нумерация элементов вектора в Mathcad по умолчанию начинается с нуля. В поле над знаком суммы вставим конечное значение индекса суммирования: 10 (по количеству элементов в векторе  , начиная с нуля).
, начиная с нуля).
· Аналогично определить  .
.
· Определить коэффициенты многочлена приближения. Коэффициенты находятся путем решения нормальной системы линейных уравнений вида (4). Количество уравнений в системе и количество искомых коэффициентов (переменных системы) определяется степенью искомого многочлена приближения, степень задается заранее. В нашем примере задана первая степень многочлена приближения, поэтому искомый многочлен имеет вид:  . Следовательно, для определения
. Следовательно, для определения  и
и  нужно решить систему двух линейных уравнений с двумя неизвестными. Значения коэффициентов при неизвестных этой системы уравнений определены нами ранее как
нужно решить систему двух линейных уравнений с двумя неизвестными. Значения коэффициентов при неизвестных этой системы уравнений определены нами ранее как  - элементы матрицы S. Значения правых частей системы уравнений также определены нами как
- элементы матрицы S. Значения правых частей системы уравнений также определены нами как  - элементы вектора T. Поэтому систему линейных уравнений для определения коэффициентов многочлена первой степени можно записать следующим образом:
- элементы вектора T. Поэтому систему линейных уравнений для определения коэффициентов многочлена первой степени можно записать следующим образом:  . Неизвестными являются элементы вектора А. Найдем их, используя обратную матрицу
. Неизвестными являются элементы вектора А. Найдем их, используя обратную матрицу 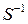 .
.
Получим:  . Запишем эту формулу на новой строке рабочего пространства Mathcad. Чтобы увидеть значения коэффициентов многочлена, введите
. Запишем эту формулу на новой строке рабочего пространства Mathcad. Чтобы увидеть значения коэффициентов многочлена, введите  . Mathcad отобразит элементы вектора А.
. Mathcad отобразит элементы вектора А.
· Записать формулу многочлена следующим образом:
 .
.
При помощи этой формулы можно определить любое промежуточное значение заданной табличной функции.
Результат на экране (для m=1):


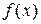 задана в виде табл. 1.
задана в виде табл. 1.
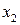




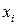 - аргумент функции;
- аргумент функции; - значение функции.
- значение функции. , чтобы среднеквадратическое уклонение найденных значений от заданных было минимальным, т.е. чтобы соблюдалось соотношение:
, чтобы среднеквадратическое уклонение найденных значений от заданных было минимальным, т.е. чтобы соблюдалось соотношение: (1)
(1) (2)
(2) сводится к определению таких его коэффициентов
сводится к определению таких его коэффициентов  , чтобы значение среднеквадратического уклонения
, чтобы значение среднеквадратического уклонения  для этого многочлена было минимальным. Для решения задачи будем использовать необходимое условие экстремума функции
для этого многочлена было минимальным. Для решения задачи будем использовать необходимое условие экстремума функции 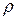 . Найдем экстремум функции, аргументами которой являются
. Найдем экстремум функции, аргументами которой являются  (3)
(3) (4)
(4) (5)
(5) , находим коэффициенты искомого многочлена. Количество уравнений в системе и количество искомых коэффициентов (переменных системы) определяется степенью искомого многочлена приближения. После вычисления коэффициентов многочлена необходимо вычислить величину среднеквадратического уклонения
, находим коэффициенты искомого многочлена. Количество уравнений в системе и количество искомых коэффициентов (переменных системы) определяется степенью искомого многочлена приближения. После вычисления коэффициентов многочлена необходимо вычислить величину среднеквадратического уклонения 

 задана таблицей:
задана таблицей: ;
;
 . Для определения нижних индексов воспользуемся клавишей ([). Для ввода оператора суммирования воспользуемся палитрой вычислений (Calculus Palette) или комбинацией клавиш (Ctrl+Shift+4). Появится оператор суммирования с четырьмя полями для ввода данных. Вставим в поле ввода справа от знака суммы
. Для определения нижних индексов воспользуемся клавишей ([). Для ввода оператора суммирования воспользуемся палитрой вычислений (Calculus Palette) или комбинацией клавиш (Ctrl+Shift+4). Появится оператор суммирования с четырьмя полями для ввода данных. Вставим в поле ввода справа от знака суммы 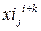 , так как необходимо суммировать вектора
, так как необходимо суммировать вектора  . В левое поле под знаком суммы введем индекс суммирования j, а в правое – начальное значение этого индекса, равное 0. Суммирование производится по количеству элементов вектора
. В левое поле под знаком суммы введем индекс суммирования j, а в правое – начальное значение этого индекса, равное 0. Суммирование производится по количеству элементов вектора  .
. . Следовательно, для определения
. Следовательно, для определения  и
и  нужно решить систему двух линейных уравнений с двумя неизвестными. Значения коэффициентов при неизвестных этой системы уравнений определены нами ранее как
нужно решить систему двух линейных уравнений с двумя неизвестными. Значения коэффициентов при неизвестных этой системы уравнений определены нами ранее как  . Неизвестными являются элементы вектора А. Найдем их, используя обратную матрицу
. Неизвестными являются элементы вектора А. Найдем их, используя обратную матрицу 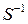 .
. . Запишем эту формулу на новой строке рабочего пространства Mathcad. Чтобы увидеть значения коэффициентов многочлена, введите
. Запишем эту формулу на новой строке рабочего пространства Mathcad. Чтобы увидеть значения коэффициентов многочлена, введите  . Mathcad отобразит элементы вектора А.
. Mathcad отобразит элементы вектора А. .
.



