Задание № 3. Определить порядок многочлена, дающего большее приближение.
· Определить величину среднеквадратического уклонения
Чтобы увидеть значение среднеквадратического уклонения для найденного многочлена первой степени, введем · Изменить запись в Mathcad так, чтобы найти многочлен второй степени. Для этого в определении степени искомого полинома m измените 1 на 2. Пересчет произойдет автоматически. Изменится и значение среднеквадратического уклонения, оно стало меньше. Это признак того, что многочлен второго порядка имеет большее приближение. · Измените в определении m на 3, а затем на 4. обратите внимание на изменения графика и значения среднеквадратического уклонения при m=4. График многочлена и исходные точки теперь совпадают, значение среднеквадратического уклонения возросло в десятки раз. Вывод, что многочлен четвертой степени дает слишком малое приближение для исходной табличной функции будет неверен, так как это вычислительный эффект, связанный с неточностью решения системы линейных уравнений (СЛУ).
Результат на экране
|
для оценки степени приближения многочлена. Запишем: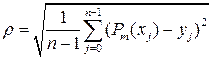
.
.
