Кривые второго порядка (на плоскости)
Эллипс.
Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек плоскости  и
и  , называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
Постоянную сумму расстояний произвольной точки эллипса до фокусов принято обозначать через  . Расстояние между фокусами равно
. Расстояние между фокусами равно  .
.
Если фокусы эллипса совпадают, то он представляет собой окружность.
Расположим эллипс так, чтобы его фокусы лежали на оси абсцисс симметрично относительно оси ординат, то есть 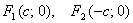 (Рис.1). Пусть
(Рис.1). Пусть  текущая точка эллипса. В этой системе координат уравнение эллипса имеет вид:
текущая точка эллипса. В этой системе координат уравнение эллипса имеет вид:
 , (1)
, (1)
где 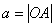 - большая,
- большая, 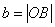 - малая полуоси эллипса,
- малая полуоси эллипса,  . Центр симметрии эллипса, определяемого уравнением (2.12.1), совпадает с началом координат. Уравнение вида (1) называется каноническим уравнением эллипса. Это уравнение второй степени, следовательно, эллипс – кривая второго порядка.
. Центр симметрии эллипса, определяемого уравнением (2.12.1), совпадает с началом координат. Уравнение вида (1) называется каноническим уравнением эллипса. Это уравнение второй степени, следовательно, эллипс – кривая второго порядка.

Рис.1.
Эксцентриситетом эллипса называется число 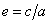 , равное отношению фокусного расстояния к большой полуоси эллипса. Для эллипса -
, равное отношению фокусного расстояния к большой полуоси эллипса. Для эллипса -  (для окружности -
(для окружности -  ). Отрезки
). Отрезки  и
и  называются фокальными радиусами точки М и могут быть вычислены по формулам
называются фокальными радиусами точки М и могут быть вычислены по формулам  и
и 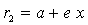 . Если эллипс определен уравнением (1) и
. Если эллипс определен уравнением (1) и  , то прямые
, то прямые  называются директрисами эллипса (если
называются директрисами эллипса (если 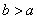 , то директрисы определяются уравнениями
, то директрисы определяются уравнениями  ).
).

 и
и  , называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами. . Расстояние между фокусами равно
. Расстояние между фокусами равно  .
.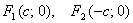 (Рис.1). Пусть
(Рис.1). Пусть  текущая точка эллипса. В этой системе координат уравнение эллипса имеет вид:
текущая точка эллипса. В этой системе координат уравнение эллипса имеет вид: , (1)
, (1)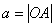 - большая,
- большая, 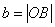 - малая полуоси эллипса,
- малая полуоси эллипса,  . Центр симметрии эллипса, определяемого уравнением (2.12.1), совпадает с началом координат. Уравнение вида (1) называется каноническим уравнением эллипса. Это уравнение второй степени, следовательно, эллипс – кривая второго порядка.
. Центр симметрии эллипса, определяемого уравнением (2.12.1), совпадает с началом координат. Уравнение вида (1) называется каноническим уравнением эллипса. Это уравнение второй степени, следовательно, эллипс – кривая второго порядка.
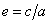 , равное отношению фокусного расстояния к большой полуоси эллипса. Для эллипса -
, равное отношению фокусного расстояния к большой полуоси эллипса. Для эллипса -  (для окружности -
(для окружности -  ). Отрезки
). Отрезки  и
и  называются фокальными радиусами точки М и могут быть вычислены по формулам
называются фокальными радиусами точки М и могут быть вычислены по формулам  и
и 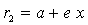 . Если эллипс определен уравнением (1) и
. Если эллипс определен уравнением (1) и  , то прямые
, то прямые  называются директрисами эллипса (если
называются директрисами эллипса (если 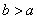 , то директрисы определяются уравнениями
, то директрисы определяются уравнениями  ).
).


