Метод наименьших квадратов в случае промежутка.
Метод наименьших квадратов в случае промежутка.
Пусть теперь функция y=f(x) задана не на стеке узлов, а на отрезке [a,b], и требуется найти её среднеквадратическое приближение в этом промежутке при помощи полинома:
В этом случае вместо конечной суммы S рассматриваем интеграл:
Подбираем коэффициенты полинома Pm(x) так, чтобы интеграл I при заданном m принимал наименьшее значение. Приравнивая нулю частные производные от I по всем ak, получим следующую систему уравнений:
или в развернутой форме:
или
т.е.
Систему (4) запишем и в более привычном виде:
Определитель этой системы запишется в виде:
Определитель (6) есть определитель Грамма. Следовательно, Подставляя найденное решение в формулу (1), получим искомый многочлен. Рассмотрим, например, случай, когда отрезок [a,b] совпадает с отрезком [-1;1] и m=4. Тогда вводя обозначения:
и вычисляя интегралы
Решая ее, находим:
В этом случае, когда при построении приближения функции f(x) при помощи Pm(x) по методу наименьших квадратов, мы по каким-либо соображениям желаем получить в одних частях рассматриваемого промежутка более точное приближение по сравнению с другими его частями, можно поступить следующим образом: интеграл I, определенный равенством («), заменяем интегралом более общего вида:
где
|

 (1)
(1)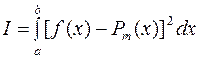 (2)
(2)
 (3)
(3)
 (4)
(4) (5)
(5) (6)
(6) , т.к. система функций
, т.к. система функций  линейно независима. Таким образом, система (5) имеет и притом единственное решение a0,a1,a2,…,am, которое, очевидно, и будет давать наименьшее значение интегралу I.
линейно независима. Таким образом, система (5) имеет и притом единственное решение a0,a1,a2,…,am, которое, очевидно, и будет давать наименьшее значение интегралу I.
 и вычисляя систему (5) в виде:
и вычисляя систему (5) в виде:

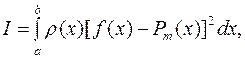 (6’)
(6’) - специальным образом подобранная неотрицательная функция, называемая весом; при этом
- специальным образом подобранная неотрицательная функция, называемая весом; при этом 


