| дата
|
|
| 16.12.13
| Знакомство с клиническим психологом ПНД №7 Рождественским Владимиром Игоревичем.
Знакомство с пациенткой и сбор анамнеза.
|
| 17.12.13.
| Знакомство с новыми пациентами- призывниками (А.и П.) и пациенткой О.
Сбор и изучение анамнеза.
|
| 18.12.13
| Посещение клинического разбора. Разбор сложных случаев, постановка диагноза.
Продолжение работы с пациентами, проведение методик. Знакомство с новой пациенткой М., сбор анамнеза.
|
| 20.12.13
| Проведение методики «Векслер» на пациенте П.
Пациент А. не пришел
|
| 23.12.13
| Проведение методики «Векслер» на пациенте А.
Испытуемая Н. проведение методик на исследование мышления.
|
| 24.12.13
| Испытуемый П. итоговая встреча. Проведение методик на исследования мышления и личности. Обнаружено преобладание истероидных черт, достигающих уровня акцентуации.
|
| 25.12.13
| Сдача заключений ЭПО куратору
Испытуемый А: Выявленные нарушения свидетельствуют об органическом типе изменения психических процессов по идеаторному (легкой степени) и амнестическому (легкая степень), астеническому (легкая степень) вариантам у личности с неустойчивым типом психопатии.
Испытуемая Н.: Выявленные нарушения свидетельствуют об изменении психических процессов по эндогенному типу у личности с психопатоподобным поведением в преморбите.
|
| 26.12.13
| Получение характеристик.
|
Министерство образования и науки РФ
Кузнецкий институт информационных и управленческих технологий
Филиал ПГУ
Кафедра ЕН и ТД
ОТЧЕТ ПО ЛАБОРАТОРНЫМ РАБОТАМ
По дисциплине
«Численные методы»
Выполнили: студенты гр. 10кр1
Швецов А.Н.
Костюньков С.А.
Принял: ст.преподователь
Кафедры ЕН и ТД
Астахова Ю.Н.
Лабораторная работа № 1
Методы решения нелинейных уравнений.
Цель работы: изучение методов решения нелинейных и трансцендентных уравнений.
Метод хорд.
Для нахождения очередного приближения корня, находящегося в интервале [ a,b ], этот интервал делят в отношении | f (a)|: |f (b)|. Тогда приближенное значение корня определяется по формуле:
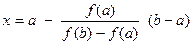 .
.
Выбирается тот из интервалов [ a,x ] или [ х,b ], в котором функция меняет свой знак, и процесс уточнения корня повторяется.
Вычисления корня нужно прекратить в том случае, когда выполняется неравенство
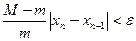 ,
,
где  ,
,  .
.

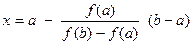 .
.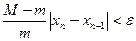 ,
, ,
,  .
.


