Пример 8.
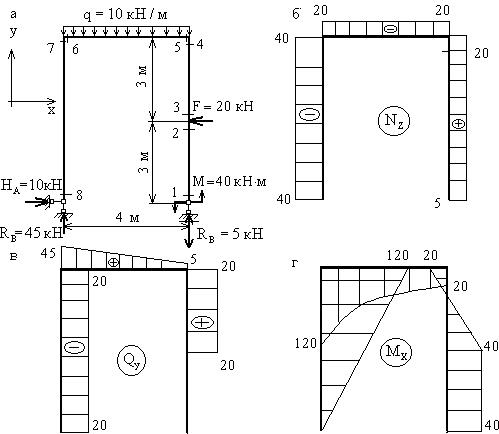
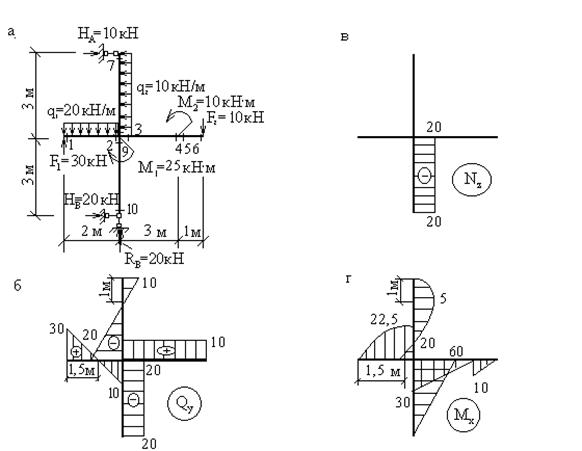
Рассмотрим раму той же конфигурации, размеров и с теми же нагрузками, что и в предыдущем примере, но с шарнирным опиранием (рис.12,а). Здесь также имеем 8 характерных сечений, но для построения эпюр необходимо вычислить сначала опорные реакции, т.к. ни для одного из сечений нельзя выбрать отсеченную часть так, чтобы избежать попадания в нее опоры с неизвестной реакцией. Для определения опорных реакций в плоских шарнирных рамах используются следующие уравнения равновесия:
Первое уравнение равновесия используется в том из двух приведенных вариантов, который будет содержать одну неизвестную опорную реакцию. Так, в рассматриваемом примере этим условием будет
Рис. 12 Второе и третье уравнения равновесия ( В качестве проверки вычисленных реакций используется условие, противоположное первому, то есть Построение эпюр Вычислим реакции опор рамы (рис.12,а) Уравнения статики:
Знак "-", полученный при вычислении реакции
то есть реакции опор вычислены правильно. Построение эпюры Двигаясь по оси рамы от сечения 1 к сечению 6, получим:
Для сечений 7 и 8 проще рассматривать отсеченную часть, продвигаясь от опоры А к сечению 7:
Этот же результат получим из рассмотрения отсеченной части 1-6:
Этот же результат получим из рассмотрения отсеченной части 1-6:
По вычисленным значениям строим эпюру Построение эпюры Из рассмотрения отсеченной части 1-5:
Из рассмотрения отсеченной части 8-6:
Эпюра Построение эпюры Из рассмотрения отсеченной части 1-5:
Из рассмотрения отсеченной части 8 -6:
(сжаты правые волокна стойки и нижние волокна ригеля в сечениях 7 и 6 соответственно). Эпюра Пример 9. Рассмотрим шарнирную раму более сложной конфигурации (рис.13,а). Здесь необходимо рассматривать 10 характерных сечений для построения эпюр Уравнения статики для вычисления опорных реакций имеют вид:
Проверка вычисления опорных реакций:
При построении эпюр
Рис. 13 Построение эпюр Из рассмотрения левой относительно центрального узла отсеченной части (сечения 1-2):
Из рассмотрения правой отсеченной части (сечения 3-6):
Из рассмотрения верхней относительно центрального узла отсеченной части (сечения 7-8):
Из рассмотрения нижней отсеченной части (сечения 9-10):
Характер эпюры Вычислим экстремальные значения момента На участках под распределенной нагрузкой
На участке с распределенной нагрузкой
Эпюры
|

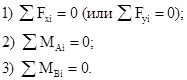
 , которое будет содержать неизвестную реакцию
, которое будет содержать неизвестную реакцию 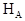 (в то время как условие
(в то время как условие  содержало бы две неизвестных реакции). Если бы опоры располагались так, что вертикальным является один стержень, то в качестве первого шага использовалось условие
содержало бы две неизвестных реакции). Если бы опоры располагались так, что вертикальным является один стержень, то в качестве первого шага использовалось условие 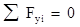 .
.
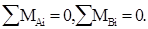 ) - такие же, как и для балок, но в одно из них обязательно войдет реакция, вычисленная из первого уравнения (иногда - с нулевым плечом).
) - такие же, как и для балок, но в одно из них обязательно войдет реакция, вычисленная из первого уравнения (иногда - с нулевым плечом). .
. в шарнирных рамах выполняется так же, как и в защемленных, но " с меньшими затратами", так как после вычисления реакций опор направление обхода рамы не играет роли, и выбор отсеченной части в каждом случае определяется ее простотой.
в шарнирных рамах выполняется так же, как и в защемленных, но " с меньшими затратами", так как после вычисления реакций опор направление обхода рамы не играет роли, и выбор отсеченной части в каждом случае определяется ее простотой.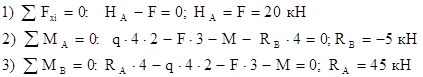
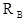 , говорит, что принятое для нее направление нужно изменить на противоположное. Выполним проверку:
, говорит, что принятое для нее направление нужно изменить на противоположное. Выполним проверку: ,
,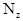 .
.
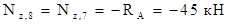

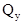 .
.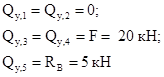

 .
. (сжаты правые волокна стойки);
(сжаты правые волокна стойки); (плечо силы F равно нулю);
(плечо силы F равно нулю); (сжаты левые волокна стойки в сечении 4 и нижние волокна ригеля в сечении 5);
(сжаты левые волокна стойки в сечении 4 и нижние волокна ригеля в сечении 5);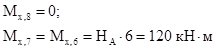
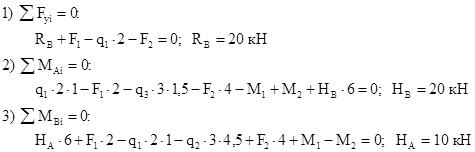

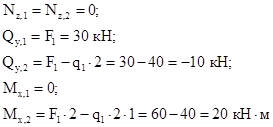 (сжаты верхние волокна).
(сжаты верхние волокна).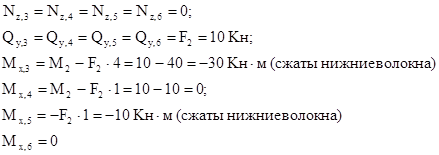
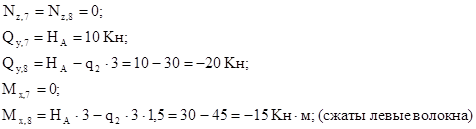
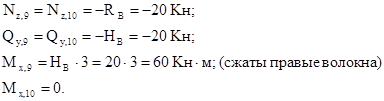
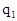 и
и 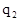 , а именно, наличие пересечений эпюры с осью рамы, говорит о том, что в этих точках момент
, а именно, наличие пересечений эпюры с осью рамы, говорит о том, что в этих точках момент 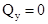 ) выполняется так же, как и в балках (см. 1.9).
) выполняется так же, как и в балках (см. 1.9).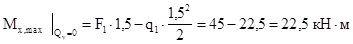 (сжаты верхние волокна).
(сжаты верхние волокна).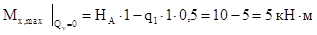 (сжаты правые волокна).
(сжаты правые волокна).


