Другие подходы к построению эпюр внутренних силовых факторовПомимо описанного выше, можно выделить еще два подхода к построению эпюр. В первом случае намечают не характерные сечения, а характерные точки, в качестве которых выделяют точки приложения сосредоточенных сил и моментов, а также точки начала и конца участков с распределенными нагрузками. Затем определяют величину внутреннего силового фактора слева и справа (бесконечно близко) от характерной точки. Другой возможный подход состоит в том, что балка разбивается на участки (с распределенными нагрузками и между точками приложения сил и моментов). Для каждого участка записывается выражение внутреннего силового фактора в общем виде как функции координаты z. Затем вычисляются значения на концах каждого участка. Очевидно, что при обоих подходах в конечном счете все сводится к вычислению внутренних силовых факторов в характерных сечениях, то есть соответствует описанному выше способу, но требует дополнительной, как правило неоправданной, работы. Правда, следует отметить, что запись общих выражений как функций от z удобна при программировании построения эпюр при помощи вычислительной техники. 1.13 Построение эпюр для плоских рам Плоской рамой называется стержневая система, элементы которой жестко или шарнирно соединены между собой, нагруженная в своей плоскости. Вертикально (или под наклоном) расположенные стержни рамы называются стойками, а горизонтальные - ригелями. Жесткость узлов устраняет возможность взаимного поворота скрепленных стержней, то есть в узловой точке углы между их осями остаются неизменными. Как и многие другие системы, рамы делятся на статически определимые и статически неопределимые (рис.10, б,в,д,е). Промежуточный шарнир снижает степень статической неопределимости рамы на величину m - 1, где m - число стержней, сходящихся в шарнире. Если m >2, то шарнир называется кратным (рис.10,д). Для определения степени статической неопределимости плоской рамы можно воспользоваться формулой: n = 3К-Ш, где n - степень статической неопределимости; К - число замкнутых контуров в предположении полного отсутствия шарниров; Ш- число шарниров в пересчете на одиночные. Основание (земля) рассматривается как стержень. Для рамы (рис.10,б) имеем: К=1; Ш=0;
Для рамы (рис.10,д): К=3; Ш=3
В более простых случаях, когда отсутствуют замкнутые контуры и промежуточные шарниры, то есть когда используются комбинации тех же опор, что и в балках (жесткая заделка, шарнирно-подвижная и шарнирно-неподвижная опоры), для определения степени статической неопределимости используется “балочная” формула:
где r - число неизвестных реакций; S - число уравнений статики (для плоской рамы S=3). В данной работе ограничимся рассмотрением простейших статически определимых рам трех видов: 1) с жесткой заделкой; 2) на двух шарнирных опорах (неподвижной и подвижной); 3) на двух шарнирно неподвижных опорах с простым промежуточным шарниром.
Рис. 10 Из шести внутренних силовых факторов в сечениях плоской рамы в общем случае возникают три: продольная сила Правила знаков. Для
Ординаты эпюр Для изгибающих моментов специального правила знаков нет, а при вычислении момента в любом сечении знак принимается произвольно. Но результат вычислений всегда откладывается со стороны сжатого волокна элемента рамы. При этом знак на эпюре
|
,
; поперечная сила 
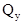; изгибающий момент 
.
, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, вызывает в данном сечении растяжение и 
- в противном случае.
, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, стремится повернуть данное сечение по часовой стрелке и 
- в противном случае.
