Балки на двух опорах
В отличие от консольных балок, при расчете балок на двух шарнирных опорах необходимо сначала определить опорные реакции из уравнений статики, так как и в левую, и в правую отсеченные части для любого сечения, расположенного между опорами, попадает соответствующая реакция. Для плоской системы число уравнений статики в общем случае равно трем. Если балка загружена только вертикальными нагрузками, то горизонтальная реакция шарнирно-неподвижной опоры равна нулю, и одно из уравнений равновесия
Условие Пример 5. Построить эпюры Порядок расчета. 1. Вычисляем реакции опор.
Проверка:
2. Намечаем характерные сечения. В отличие от консольных балок здесь известны обе опорные реакции, поэтому для любого сечения можно рассматривать как левую, так и правую отсеченную часть. 3. Определяем поперечные силы в характерных сечениях.
Строим эпюру 4. Определяем изгибающие моменты в характерных сечениях.
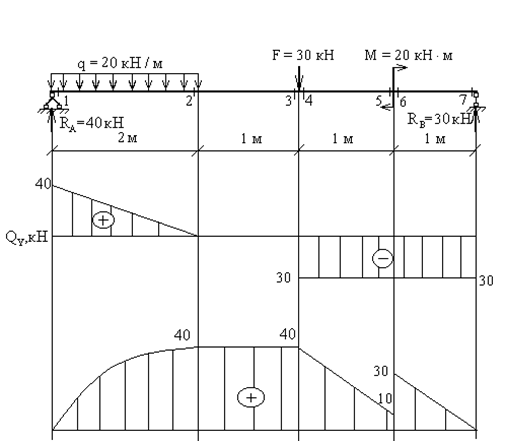
Рис. 8 Строим эпюру Пример 6. Построить эпюры Порядок расчета. 1. Вычисляем опорные реакции.
Во втором уравнении равновесия (впрочем, как и в первом) момент от распределенной нагрузки
Рис.9 Вычисленное из этого уравнения значение реакции Проверка:
2. Намечаем характерные сечения. 3. Вычисляем поперечную силу и изгибающий момент в характерных сечениях. Из рассмотрения левой отсеченной части:
Для сечений 5-7 удобнее рассматривать правую отсеченную часть:
По вычисленным значениям строим эпюры 1.11 Правила контроля эпюр Qу и Mx Дифференциальные зависимости между 1. Эпюра 2. Под точкой приложения сосредоточенной силы (реакции) на эпюре 3. Если на участке под распределенной нагрузкой эпюра 4. На участках с поперечной силой одного знака эпюра 5. Порядок линии на эпюре
|

 обращается в тождество. Таким образом, для определения реакций в опорах шарнирной балки используются два уравнения статики:
обращается в тождество. Таким образом, для определения реакций в опорах шарнирной балки используются два уравнения статики: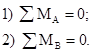
 используется для проверки вычисленных значений опорных реакций.
используется для проверки вычисленных значений опорных реакций. для балки с шарнирным опиранием (рис.8).
для балки с шарнирным опиранием (рис.8).
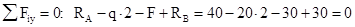

 .
.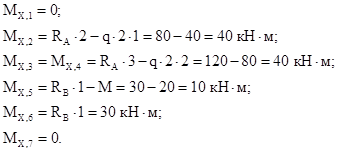


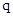 вычислен без разбиения ее на две части - слева и справа от опоры В, то есть определена равнодействующая нагрузки
вычислен без разбиения ее на две части - слева и справа от опоры В, то есть определена равнодействующая нагрузки 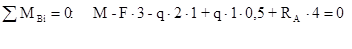

 , разумеется, совпадает с полученным ранее.
, разумеется, совпадает с полученным ранее.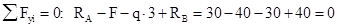
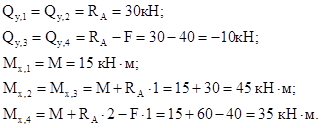

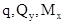 определяют ряд закономерностей, которым подчиняются эпюры
определяют ряд закономерностей, которым подчиняются эпюры  обязателен скачок на величину момента.
обязателен скачок на величину момента.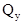 пересекает ось
пересекает ось 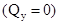 , то эпюра
, то эпюра  эпюра
эпюра  - убывает.
- убывает.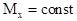 (прямая, параллельная оси), то на этом участке
(прямая, параллельная оси), то на этом участке 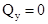 .
.


