При построении эпюр 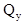 и
и  в консольных, или жестко защемленных, балках нет необходимости (как и в рассмотренных ранее примерах) вычислять опорные реакции, возникающие в жесткой заделке, но выбирать отсеченную часть нужно так, чтобы заделка в нее не попадала.
в консольных, или жестко защемленных, балках нет необходимости (как и в рассмотренных ранее примерах) вычислять опорные реакции, возникающие в жесткой заделке, но выбирать отсеченную часть нужно так, чтобы заделка в нее не попадала.
Пример 3. Построить эпюры 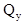 и
и  (рис.6).
(рис.6).

Рис. 6
Порядок расчета.
1. Намечаем характерные сечения.
2. Определяем поперечную силу 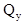 в каждом характерном сечении.
в каждом характерном сечении.

По вычисленным значениям строим эпюру 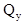 .
.
3. Определяем изгибающий момент  в каждом характерном сечении.
в каждом характерном сечении.

По вычисленным значениям строим эпюру  , причем, на участке под распределенной нагрузкой эпюра будет криволинейной (квадратная парабола). Выпуклость кривой на этом участке всегда обращена навстречу распределенной нагрузке.
, причем, на участке под распределенной нагрузкой эпюра будет криволинейной (квадратная парабола). Выпуклость кривой на этом участке всегда обращена навстречу распределенной нагрузке.
1.9 Дифференциальные зависимости между 
Указанные зависимости используются при построении эпюр  , поэтому приведем их здесь без соответствующего вывода, который дается в лекционном курсе.
, поэтому приведем их здесь без соответствующего вывода, который дается в лекционном курсе.

Пример 4. Построить эпюры  (рис.7).
(рис.7).
В данном случае для правильного построения эпюры  необходимо использовать приведенные выше дифференциальные зависимости.
необходимо использовать приведенные выше дифференциальные зависимости.
Порядок расчета.
1. Намечаем характерные сечения.
2. Определяем поперечные силы в характерных сечениях.

Строим эпюру 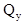 .
.
Характер эпюры, то есть тот факт, что эпюра 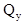 пересекает ось, говорит о том, что в этом сечении момент
пересекает ось, говорит о том, что в этом сечении момент  будет иметь экстремальное значение. Действительно, пересечение эпюры с осью z означает, что в этом сечении
будет иметь экстремальное значение. Действительно, пересечение эпюры с осью z означает, что в этом сечении  , а из курса математики известно, что если производная функции равна нулю, то сама функция в данной точке имеет экстремальное значение.
, а из курса математики известно, что если производная функции равна нулю, то сама функция в данной точке имеет экстремальное значение.
Для определения положения “нулевого” сечения необходимо величину расположенной слева от него ординаты эпюры 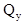 разделить на интенсивность распределенной нагрузки q:
разделить на интенсивность распределенной нагрузки q:


Рис. 7
Определяем изгибающие моменты в характерных сечениях.

4. Вычисляем экстремальное значение изгибающего момента в сечении, где  :
: 
Строим эпюру  .
.

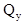 и
и  в консольных, или жестко защемленных, балках нет необходимости (как и в рассмотренных ранее примерах) вычислять опорные реакции, возникающие в жесткой заделке, но выбирать отсеченную часть нужно так, чтобы заделка в нее не попадала.
в консольных, или жестко защемленных, балках нет необходимости (как и в рассмотренных ранее примерах) вычислять опорные реакции, возникающие в жесткой заделке, но выбирать отсеченную часть нужно так, чтобы заделка в нее не попадала.



 , поэтому приведем их здесь без соответствующего вывода, который дается в лекционном курсе.
, поэтому приведем их здесь без соответствующего вывода, который дается в лекционном курсе.

 , а из курса математики известно, что если производная функции равна нулю, то сама функция в данной точке имеет экстремальное значение.
, а из курса математики известно, что если производная функции равна нулю, то сама функция в данной точке имеет экстремальное значение.


 :
: 



