Моменты распределения и средние молекулярные массы
Определение понятия средней ММ полимера при непрерывном распределении базируется на теории случайных величин, каковыми и являются значения ММ макромолекул для большинства полимеризационных процессов. В теории случайных величин существует понятие момента распределения случайной величины ω, который, применительно к рассматриваемому случаю, выражается следующим образом:
где n - любое целое число. По определению, отношение любого момента к предыдущему равно среднему значению случайной величины:
Таким образом, согласно теории случайных величин, существует множество значений средних ММ полидисперсного полимера с непрерывным распределением. Практически используют первые три члена ряда средних ММ:
Далее, учитывая (1.7) и (1.13), получаем
Выражение (1.13) по содержанию аналогично (1.5), следовательно, первое выражает среднейисловую ММ. То же самое можно сказать о (1.14) и (1.6), следовательно, (1.14) выражает среднемассовую ММ полимера. Величины
|

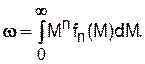 (1.8)
(1.8)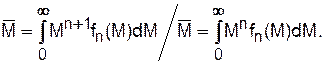 (1.9)
(1.9)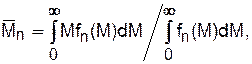 (1.10)
(1.10) (1.11)
(1.11)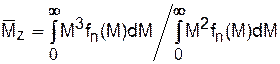 . (1.12)
. (1.12) тогда
тогда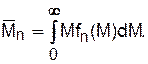 (1.13)
(1.13)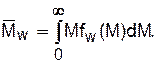 (1.14)
(1.14)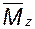 называется z - средней или среднеседиментационной ММ. Эта характеристика не имеет такого наглядного истолкования, как среднечисловая и среднемассовая ММ.
называется z - средней или среднеседиментационной ММ. Эта характеристика не имеет такого наглядного истолкования, как среднечисловая и среднемассовая ММ.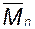 ,
,  ,
, 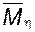 , близкой к
, близкой к 


