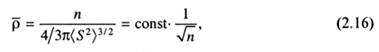Идеальный клубок
Многие свойства цепных макромолекул и полимеров в целом, а также форма и размер первых могут быть предсказаны теоретически на основе анализа модели идеальной цепи. Физической моделью идеальной цепи является свободно сочлененная цепь или цепь из «бусинок». Первая составлена из n отрезков длиной l, шарнирно соединенных друг с другом, вторая - из n «бусинок» одинаковой массы, нанизанных на гибкую нить и расположенных на расстоянии l одна от другой. Свободно сочлененная цепь. Построить такую цепь, т.е. зафиксировать одну из ее возможных конформаций, можно путем последовательного наращивания числа связанных отрезков, ориентированных случайным образом. Закрепим один конец первого отрезка в начале координат (рис. 2.1), другой его конец может находиться в любой точке сферы, описываемой радиусом l. Закрепим второй конец отрезка в точке с координатами Х1 и шарнирно соединим в этой точке первый отрезок со вторым. Свободный конец второго отрезка также может находиться в любой точке сферы, описываемой радиусом l. Первый отрезок не ограничивает ориентацию второго, поскольку цепь является бестелесной, гипотетической, что допускает наложение и пересечение отрезков. Закрепим свободный конец второго отрезка в точке с координатой Х2 и соединим с третьим отрезком. Продолжая подобную процедуру сколь угодно долго, мы можем построить фиксированную конформацию свободно сочлененной цепи с любым количеством звеньев. Для ориентации свободных концов отрезков цепи можно использовать любой механизм реализации закона случая. Положение в пространстве свободно сочлененной цепи определяется набором координат X1, Х2... Хn, а вероятность определенной конформаций - выражением:
где
Рис. 2.1. Построение свободно сочлененной цепи
Для бестелесной цепи
Поскольку Рх < 1, то
при этом
С учетом (2.2) и (2.4) число возможных конформаций свободно сочлененной цепи равно:
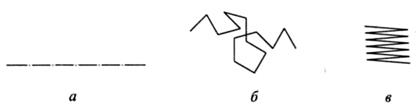
Из (2.5) следует, что с увеличением числа звеньев в цепи число возможных конформаций возрастает экспоненциально. Полученные соотношения позволяют сделать однозначный вывод о наиболее вероятном типе конформаций полимерной цепи. На рис. 2.2 приведены три типа конформаций свободно сочлененной цепи - предельно вытянутая, свернутая и плотно свернутая. В последнем случае предельно свернутая конформация будет выглядеть как одно звено, так как бестелесная свободно сочлененная цепь допускает совмещение звеньев. Поскольку вероятности всех конформаций одинаковы и чрезвычайно малы, можно с уверенностью утверждать, что вытянутые и предельно свернутые, а также близкие к ним конформаций (очень сильно вытянутые и свернутые) практически отсутствуют в конформационном наборе (множестве возможных конформаций). Число умеренно свернутых конформаций очень велико, поэтому именно они последовательно реализуются, несмотря на то, что вероятность каждой конкретной конформаций очень мала. Таким образом, анализ модели идеальной цепи приводит к выводу о том, что макромолекулы гибкоцепных полимеров свернуты в клубок. Этот вывод подтверждается экспериментально. Длина вытянутой конформаций, т.е. контурная длина цепи полимеров с молекулярной массой ~106 составляет величину порядка 103 нм. Прямые измерения показывают, что размер гибкоцепных макромолекул в растворах и полимерных телах ограничен пределами 10-100 нм. Из этого следует, что для макромолекул предпочтительны свернутые конформаций.
Рис. 2.2. Предельно вытянутая (л), свернутая (б) и плотно свернутая (сложенная) (в) конформаций свободно сочлененной цепи
Идеальный (гауссов) клубок. Размер идеальной цепи характеризуется расстоянием между ее концами. Обозначим эту величину, отвечающую конкретной конформации, через R, а величину, усредненную по всем конфор-мациям, через ‹ R 2›1/2. При теоретическом рассмотрении идеальной цепи расстояние между ее концами выражается вектором Для вытянутой цепи
R=nl=L, (2.6)
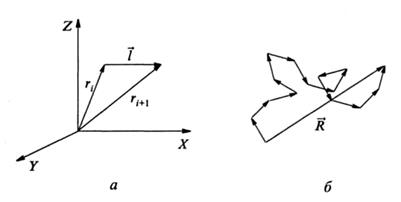
где L - контурная длина цепи. Задача установления размера свернутой свободно сочлененной цепи относится к типу задач, хорошо известных в физике. Такая задача встречалась, в частности, при описании броуновского движения, поэтому она известна как задача «случайного блуждания». Представим координаты начала и конца звеньев цепи радиусами-векторами ri, и ri+ 1 (рис. 2.3, а). Тогда звено цепи будет являться вектором
тогда
где
Рис. 2.3. Построение свободно сочлененной цепи в векторной форме
Таблица 2.1 Невозмущенные размеры клубков поли-2-винилнафталина в идеальном растворителе толуол-декалин, 30,2 °С
В свободно сочлененной цепи ориентация отрезков случайна и не скоррелирована, угол θ между векторами равновероятное значение от 0 до 2π, а косинус угла - от 1 до -1. Следовательно, усредненное значение ‹cosθ ij;› = 0, поэтому имеем:
или
«Правило квадратного корня», выведенное теоретически на основе физической модели свободно сочлененной цепи, выполняется и для реальных макромолекул, находящихся в идеальном растворителе, понятие о котором будет рассмотрено в следующем разделе. Как следует из (2.9), при соблюдении правила «квадратного корня» Сравнение выражений (2.6) и (2.10) показывает, что среднее расстояние между концами свободно сочлененной цепи меньше по сравнению с ее контурной длиной. Это указывает на то, что подавляющее большинство конформаций такой цепи отвечает рыхлому клубку. Выражение (2.10) иногда называется «правилом квадратного корня». По форме оно напоминает известное соотношение Эйнштейна-Смолуховского для среднего смещения частицы при броуновском движении: Среднеквадратичное расстояние между концами цепи является наиболее фундаментальной, но не единственной характеристикой размера цепи. Экспериментально размер цепи определяется методами светорассеяния, вискозиметрии и скоростной седиментации. При упругом рассеянии света, когда
Рис. 2.4. К понятию о радиусе инерции макромолекулы
длины волн падающего и рассеянного света одинаковы, определяется радиус инерции макромолекулы:
где ri, - расстояние от центра массы макромолекулы до каждого из ее звеньев. Иллюстрацией к выражению (2.11) является рис. 2.4. Две фундаментальные характеристики размеров макромолекул связаны соотношением Дебая:
Следует иметь в виду, что для разветвленных цепей единственной характеристикой размера является радиус инерции. Для полного представления о геометрических характеристиках макромолекулы необходимо знать не только ее средний наиболее вероятный размер, но и распределение по размерам. Из изложенного ясно, что размер цепи является случайной величиной, а число конформаций очень велико. Это дает основание применить центральную предельную теорему вероятностей, согласно которой распределение большого числа случайных величин является гауссовым, т.е. экспоненциальным. В результате почти сразу получаем:
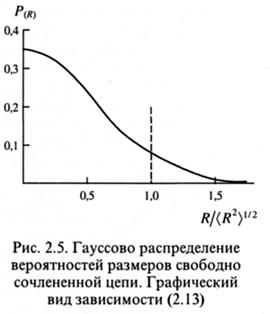
или
где P(R) - вероятность пребывания макромолекулы в состоянии с заданным R. Предэкспоненциальный множитель в выражении (2.13) устанавливается из условия нормировки: ∫; P(R)·d3x = 1. Клубок, для которого выполняется соотношение (2.13), называется идеальным или гауссовым. На рис. 2.5 приведена зависимость, соответствующая формуле (2.13). Видно, что при R > P(R) ≠ 0 при
Плотность звеньев в клубке. Для понимания особенностей строения макромолекулы очень важно знать распределение плотности звеньев в образованном ею клубке. В результате теоретических расчетов было показано, что распределение плотности звеньев в клубке относительно центра его массы близко к гауссовому:
где ρ(S) - плотность звеньев, т.е. число звеньев, приходящихся на единицу объема, S - расстояние от центра массы клубка. Рассмотрим конкретный пример гибкоцепного полимера -(СН2-СНХ) n -со степенью полимеризации р = 1000, что соответствует М ≈ 105 для таких распространенных полимеров, как полиметилметакрилат или полистирол. На рис. 2.6 приведены зависимости плотности мономерных звеньев от расстояния от центра массы клубка. Из рис. 2.6 следует, что плотность звеньев максимальна в области, близкой к центру массы клубка, и быстро уменьшается к его периферии. Средняя плотность звеньев в клубке может быть рассчитана путем деления числа звеньев на объем сферы, очерченной радиусом инерции. В результате получаем соотношение:
из которого следует, что средняя плотность звеньев в клубке обратно пропорциональна квадратному корню из числа его звеньев или молекулярной массы.
Переходя от модели идеальной цепи к реальным макромолекулам, следует отметить, что для последних характерны несколько вытянутые конформации вдоль оси, соединяющей концы цепи. Таким образом, «мгновенный» снимок такой макромолекулы по форме будет напоминать эллипс. Однако, благодаря микроброуновской диффузии кинетически независимых отрезков цепи, называемых сегментами, ее конформация постоянно изменяется, поэтому усредненная по времени форма макромолекулярного клубка близка к сферической.
|

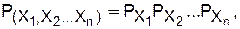 (2.1)
(2.1) ,
, 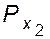 …
… 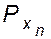 - вероятности определенной ориентации отрезков цепи.
- вероятности определенной ориентации отрезков цепи.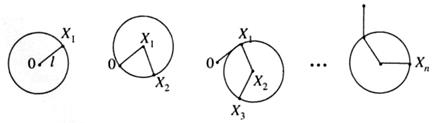
 =... =
=... = 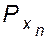 = Рх, откуда
= Рх, откуда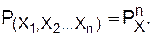 (2.2)
(2.2) (2.3)
(2.3) (2.4)
(2.4)
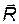 . Поскольку, ввиду случайного характера ориентации цепи, равновероятны значения
. Поскольку, ввиду случайного характера ориентации цепи, равновероятны значения 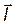 , величина и направление которого определяются условием
, величина и направление которого определяются условием 
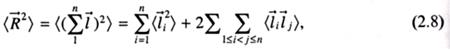

 , нм
, нм
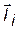 , и
, и 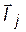 (i ≠ j) может принимать любое
(i ≠ j) может принимать любое

 , где D - коэффициент диффузии, t - время. Такое совпадение закономерно, поскольку в том и другом случае проявляется закон «случайного блуждания». По этой же причине траектория случайного блуждания броуновской частицы аналогична конформации свободно сочлененной цепи.
, где D - коэффициент диффузии, t - время. Такое совпадение закономерно, поскольку в том и другом случае проявляется закон «случайного блуждания». По этой же причине траектория случайного блуждания броуновской частицы аналогична конформации свободно сочлененной цепи.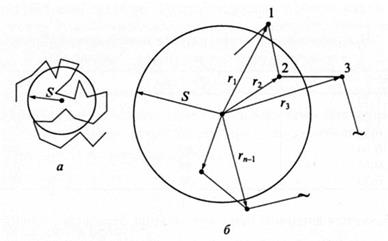


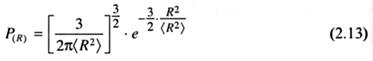
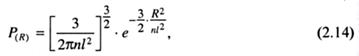
 , вероятность существования клубков быстро уменьшается с ростом R. Это соответствует сделанному ранее выводу о малой вероятности вытянутых конформаций. Бестелесность идеальной цепи объясняет
, вероятность существования клубков быстро уменьшается с ростом R. Это соответствует сделанному ранее выводу о малой вероятности вытянутых конформаций. Бестелесность идеальной цепи объясняет