Упругость идеального газа

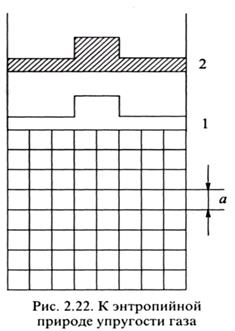
Рассмотрим один моль идеального газа, находящегося в цилиндре с поршнем (рис. 2.22), при двух состояниях: р₁, V₁ и р₂, V₂, причем р₁ > р₂ и V₁ < V₂.

Из опыта известно, что самопроизвольно газ может только расширяться, следовательно, состояние 2 термодинамически более выгодно. Причина этого заключается в том, что более разряженное состояние газа характеризуется большей термодинамической вероятностью и, следовательно, большей энтропией. Для расчета термодинамической вероятности используем простейшую объемную решетку, полагая, что в каждой ее ячейке объемом а³ (а - длина ребра кубической ячейки) находится одна молекула газа. Тогда для состояния 1 число способов расположения N молекул газа в объеме V₁ трактуемое в данном случае как термодинамическая вероятность, равно (V₁/ a ³)^N, а для состояния 2 - (V₂/ a ³)^N. Следовательно, относительное изменение термодинамической вероятности газа при переходе из состояния 1 в состояние 2 можно оценить отношением:

Поскольку V₂/V₁ > 1 и N >> 1, то число W₂/W₁ очень велико, например, при V₂/V₁ = 1,01, W₂/W₁ = .

Таким образом, чтобы деформировать (сжать) газ, нужно увеличить давление, т.е. приложить силу. После прекращения воздействия газ самопроизвольно расширится до исходного состояния, которому отвечают большая термодинамическая вероятность и, следовательно, энтропия. Если при фиксированном объеме газ нагревать, то его давление увеличится. В результате для его сжатия следует приложить большее усилие, что означает увеличение модуля упругости газа с ростом температуры.
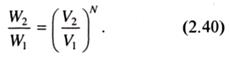
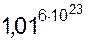