Упругость идеального клубка

 

Первая теория эластичности каучука, так называемая кинетическая теория, была предложена в 1932 г. швейцарским ученым Мейером, далее она получила развитие и подтверждение в работах Марка, Джоуля, Куна. В этой теории предполагается, что энтропия каучука складывается аддитивно, исходя из энтропии отдельных цепей. Этот принцип позволяет, учитывая молекулярно-кинетическое движение сегментов макромолекул, сразу же выявить причину обратимости высокоэластической деформации в каучуках.

Как термодинамическая система, изолированный макромолекулярный клубок напоминает газовое облако, в котором роль молекул выполняют кинетически не зависимые отрезки цепи - сегменты. Самопроизвольное тепловое движение сегментов не меняет внутренней энергии системы, поэтому

 

 

Энтропию идеальной цепи можно вычислить, исходя из уравнения Больцмана:

 

 

где W - термодинамическая вероятность. В данном случае речь идет о конформационной энтропии, т.е. энтропии, связанной с возможностью реализации клубком множества конформаций. Величина W пропорциональна числу конформаций, возможных при заданном R. Поэтому W ~ P_(R). Учитывая это и привлекая (2.13), имеем:

 

 

Подставляя (2.43) в (2.41), получаем:

 

 

Растяжение клубка под действием внешней силы приводит к отклонению R от наиболее вероятной величины , уменьшению числа возможных конформаций и, следовательно, уменьшению энтропии.

 

 

Последнее прямо следует из формулы (2.43). В результате, возникает упругая сила, противодействующая растягивающей и стремящаяся вернуть клубок к состоянию с исходным и максимумом энтропии. Выражение для величины упругой силы может быть получено, исходя из следующих соображений. Допустим, что один конец цепи закреплен, а к другому приложена сила ƒ (рис. 2.23).

Под действием этой силы конец цепи стремится на расстояние dx, дальнейшему смещению будет препятствовать упругая сила -ƒ, равная по величине, но противоположная по направлению приложенной силе. Поскольку при V = const, F = dƒ;/ dx и в данном случае dx = dR, то

 

 

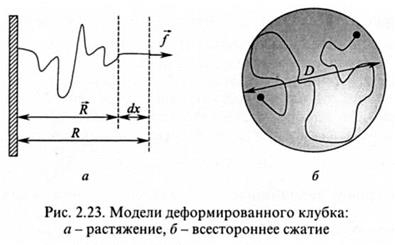
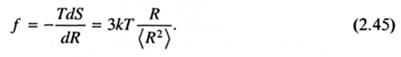
В рассматриваемой модели векторы и 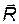параллельны. Поэтому отношение R/ 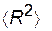можно рассматривать как относительную деформацию, и тогда уравнение (2.45) по содержанию становится аналогичным уравнению Гука. Из этой аналогии следует, что модуль упругости изолированного идеального клубка пропорционален 3 kТ, следовательно, он увеличивается с повышением температуры. Такое поведение также характерно для идеального газа. При сжатии клубка изменение функции Гиббса удобнее оценивать, пользуясь другой моделью. Рассмотрим идеальный гауссов клубок, содержащий п звеньев, помещенный внутрь непроницаемой для него сферы с диаметром D, причем

 

 

D < (рис. 2.23, б). Очевидно, что в таких условиях цепь будет касаться стенок сферы в нескольких точках. Пусть средний отрезок цепи, заключенный между двумя контактами со стенкой, содержит в среднем n * звеньев. Тогда, очевидно, что число контактов клубка со сферой равно n / n * и на каждом из этих контактов макромолекулярный клубок теряет половину своего конформационного набора (Это становится ясно при выполнении процедуры построения свободно сочлененной цепи, рассмотренной в разд. 2.1.1 с учетом выражений (2.1), (2.2) и (2.5).). Следовательно, изменение энтропии, вызванное сжатием клубка в сфере, исходя из формулы Больцмана, будет равно:

 

где S и S₀ - энтропия деформированного и невозмущенного клубка.

 

Таким образом, как растяжение, так и сжатие клубка приводят к уменьшению энтропии и возникновению упругой силы, которая стремится вернуть систему к исходному состоянию с максимумом энтропии, соответствующему среднеквадратичному размеру недеформированного клубка (рис. 2.24).