Модель Максвелла. Релаксация напряжения
Идеально упругое тело. Поведение идеально упругого тела описывается законом Гука (2.39), а универсальной характеристикой упругости является модуль Юнга Е - коэффициент пропорциональности между деформацией и напряжением. Ньютоновская жидкость. Основным законом, описывающим течение «идеальной», так называемой ньютоновской жидкости, является закон Ньютона-Стокса, иллюстрацией к которому служит рис. 2.27. Слой жидкости толщиной d помещен между двумя плоскопараллельными пластинами, из которых одна с площадью S является подвижной, другая - неподвижной. К верхней подвижной пластине приложена сила ƒ, под действием которой она движется со скоростью v. Благодаря трению, движение передается жидкости, слои которой движутся с убывающей скоростью. Сила ƒ и скорость v связаны уравнением:
где ŋ - коэффициент пропорциональности, называемый вязкостью, который характеризует внутреннее трение в жидкости при ее течении.
Из рис. 2.27 видно, что слои жидкости вовлекаются в течение путем приложения к ним силы (трения) по касательной. В этом случае приложенная сила, отнесенная к единице площади, называется напряжением сдвига, а градиент скорости в направлении, перпендикулярном приложенной силе (потока), - скоростью сдвига. С учетом сказанного уравнение Ньютона-Стокса можно переписать в следующем виде:
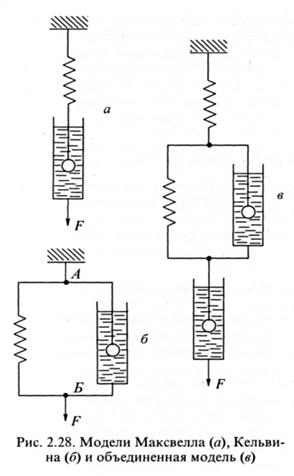
где σ = ƒ/ S - напряжение сдвига, ŋ = v / d - скорость сдвига. Жидкости, вязкость которых не зависит от напряжения сдвига, называются ньютоновскими. К ньютоновским жидкостям относят растворы полимеров с малой концентрацией растворенного вещества. Упруговязкая жидкость, т.е. жидкость, при течении которой накапливаются упругие (обратимые) деформации, может быть представлена механической моделью Максвелла (рис. 2.28), которая состоит из последовательно соединенных пружины (упругий элемент) и демпфера - поршня, передвигающегося в цилиндре с вязкой жидкостью (элемент, представляющий необратимую деформацию).
При нагружении модели поршень передвигается в цилиндре с вязкой жидкостью. За счет силы трения движение передается пружине, которая растягивается на определенную величину, запасая упругую энергию. По окончании деформации модели пружина возвращается к исходному состоянию, высвобождая запасенную упругую энергию (упругое последействие), а смещение поршня в цилиндре необратимо. К упруговязким жидкостям относятся достаточно концентрированные растворы полимеров, жидкие каучуки, расплавы полимеров. Рассмотрим простой опыт, который доказывает наличие упругого последействия в подобных жидкостях. На рис. 2.29 изображена система из двух коаксиальных цилиндров, способных к независимому вращению. Эта система является прообразом ротационного вискозиметра, широко применяемого на практике для измерения вязкости.
Если в зазор между цилиндрами поместить ньютоновскую жидкость, то при вращении внутреннего цилиндра внешний цилиндр также будет вращаться с некоторой постоянной, но меньшей скоростью за счет трения перемещающихся слоев жидкости. При прекращении вращения внутреннего цилиндра внешний сразу остановится. В случае упруговязкой жидкости по прекращении вращения внутреннего цилиндра внешний останавливается не сразу. Перед остановкой он повернется на несколько градусов в обратную сторону, что является доказательством наличия упругости у жидкости. Выше упоминалось, что параметрами, характеризующими упругое тело и ньютоновскую жидкость, являются модуль упругости Е и вязкость ŋ. Какой параметр характеризует упруцовязкую жидкость? Ответить на этот вопрос можно с помощью модели, легко поддающейся математическому описанию. Обозначим модуль упругости пружины через E, вязкость демпфера через ŋ, суммарное напряжение на пружине и поршне - через σ. Тогда, с учетом уравнений (2.39) и (2.58), скорость развития деформации ε можно описать следующим соотношением:
Рассмотрим случай, когда деформация модели фиксируется, т.е. ε = const и напряжение начнет постепенно уменьшаться в результате возвращения пружины к исходному состоянию. Процесс этот является замедленным, поскольку связан с перемещением поршня в вязкой жидкости. Если в начальный момент, отвечающий фиксации деформации, t = 0, ε = ε0 > σ = σ0 и d ε / dt = 0, то в результате интегрирования уравнения (2.60) получаем:
Параметр
|







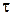 называется временем релаксации. Согласно (2.62),
называется временем релаксации. Согласно (2.62), 


