Упругость полимерной сетки
Чрезвычайно важное в практическом отношении свойство эластичности материально реализуется в резинах, т. е. сшитых каучуках, которые мы далее будем называть полимерными сетками. При теоретическом рассмотрении свойств полимерных сеток в условиях, когда реализуется подвижность сегментов (концентрированные растворы, гели, эластомеры), исходят из того, что отрезок цепи между двумя соседними сшивками, называемый субцепью, сворачивается в клубок, называемый субклубком, свойства которого аналогичны свойствам невозмущенного гауссового клубка. Такая модель позволяет качественно объяснить природу упругости резин аналогично тому, как это было сделано в предыдущем случае, т.е. как энтропийную. При действии приложенного напряжения, например растягивающего, размеры субклубка увеличиваются, что вызывает возникновение упругой силы, стремящейся вернуть клубки к исходному состоянию. По прекращении воздействия субклубки возвращаются к исходным размерам, при этом энтропия достигает максимально возможного значения. Для количественного описания упругости полимерной сетки представим ее определенный объем в виде параллелепипеда, стороны которого ориентированы вдоль осей координат (рис. 2.25).
При растяжении сетки ее размеры вдоль каждой из осей
где λx, λy, λz, - так называемые коэффициенты вытяжки. Изменение размеров сетки приводит к изменению размеров субклубков. Размер последних так же, как и в случае изолированной цепи, может быть охарактеризован радиусом-вектором,
При деформации сетки проекции Rox, R0Y, Roz изменяются в такой же степени, как и линейные размеры сетки в направлении осей координат:
Rx = Rox·λx, Ry = Roy·λy, Rz= Roz · λz
Изменение энтропии субклубка при изменении его размеров от R 0 до R, вызванном деформацией, можно учесть с помощью выражения (2.43), связывающего энтропию изолированного гауссового клубка с его размерами. В результате имеем:
где n - число звеньев в субцепи, l - длина звена. Далее необходимо перейти от отдельной субцепи к полимерной сетке. Для этого выражение (2.49) необходимо умножить на число субцепей в единице объема v, равное количеству сшивок, и на общий объем полимерной сетки V. Кроме того, нужно учесть, что все направления равновероятны, и поэтому, с учетом (2.48),
На практике наиболее часто встречается одноосное растяжение или сжатие, например вдоль оси X. Связанные с этим возможности изменения размеров сетки вдоль других осей легко установить, исходя из того фундаментального факта, что каучук и резина при деформации не изменяют объема. Отсюда легко рассчитать, что если λx = λ, то λy = λz = λ-1/2. После подстановки этих значений в уравнение (2.50) получаем:
Ранее было показано, что при растяжении гауссовой цепи Δ F = - Т ·Δ S, ƒ = -∂ F /∂ R. Применительно к рассматриваемой системе упругая сила может быть представлена выражением:
Для того, чтобы перейти к напряжению, необходимо разделить прилагаемую силу, равную по величине, но противоположную по знаку (направлению) силе упругости, на площадь образца:
Раскрывая значение производной
Соотношение (2.54) является одним из главных результатов теории эластичности полимерных сеток. Следующая из него зависимость деформации резин от величины приложенного напряжения в основном соответствует экспериментальным данным в области 5 > λ > 1 (рис. 2.26).
Выражение для модуля упругости может быть получено из (2.54) для области малых деформаций, когда можно приближенно принять
что ведет к
Величина
где v - количество сшивок в единице объема. Из уравнения (2.57) следует: упругость полимерной сетки, определяемая величиной модуля, пропорциональна количеству сшивок в единице объема; модуль упругости полимерной сетки повышается с увеличением температуры. Таким образом, из рассмотренного следует, что газы и каучуки, в том числе и «сшитые» (резины), имеют сходные харак теристики упругости - их модули упругости близки и в обоих случаях повышаются с увеличением температуры; кроме того, известно, что сжатие приводит к повышению температуры как газов, так и каучуков. Эта аналогия объясняется одинаковой природой упругости, которая, с одной стороны, может быть охарактеризована как энтропийная, с другой - как молекулярно-кинетическая. Первое указывает на природу обратимости деформации, второе - на способ ее реализации, который связан с перемещением молекул газа и сегментов молекул.
|


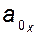 ,
,  ,
,  изменяются соответственно в λx, λy, λz раз:
изменяются соответственно в λx, λy, λz раз:
 который связан с его проекциями на оси координат соотношением:
который связан с его проекциями на оси координат соотношением:

 . Тогда для полимерной сетки в целом
. Тогда для полимерной сетки в целом



 окончательно имеем:
окончательно имеем:



 является относительным удлинением, следовательно, модуль упругости полимерной сетки равен
является относительным удлинением, следовательно, модуль упругости полимерной сетки равен



