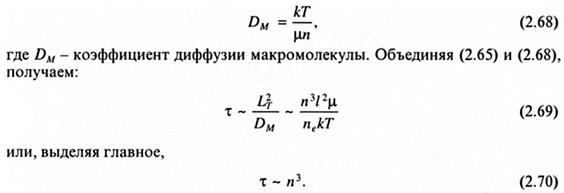Теория рептаций
Из уравнения (2.63) следует, что свойства упруговязкой жидкости определяются временем релаксации
их физическую модель. Первое положение, касающееся этой модели, состоит в том, что в концентрированных растворах и расплавах полимеров макромолекулы образуют сплошную флуктуационную сетку зацеплений, подобных тем, что изображены на рис. 2.30. Образование такой сетки объясняет возникновение упругих свойств у раствора при достижении определенной концентрации полимера. Второе положение касается характера движения макромолекул в окружении себе подобных. Согласно теории рептаций, разработанной в 70-х годах XX века Де Женом, Эдвардсом и Доем, макромолекула в таких условиях движется подобно ужу в куче хвороста, т.е. совершает змееподобные движения в трубке, образованной окружением других макромолекул. Рассмотрим механизм образования трубки. Для этого необходимо представить, что конформации всех цепей, кроме рассматриваемой нами так называемой «пробной», заморожены. Это и приведет к образованию трубки, поскольку «пробная» макромолекула не может двигаться в направлении, перпендикулярном оси трубки, она может двигаться лишь вдоль этой оси путем змееподобной диффузии, называемой рептацией. Расчеты показывают, что «размораживание» конформации соседних цепей принципиально не изменяет ситуацию - основным способом перемещения макромолекул остается рептация. Соседние цепи, образующие стенки трубки, периодически обновляются. Существует характерное время при t < при t >
Для того, чтобы вычислить
который задает толщину трубки. Сама трубка при этом может быть представлена последовательностью n / ne блобов, где n - число звеньев в цепи, ее длина LT, равна:
Естественно, что длина трубки много меньше контурной длины цепи L = n·l. В современной динамической теории полимерных жидкостей, основанной на модели рептаций, принимается, что время релаксации
где Δ x - смещение в избранном направлении; D - коэффициент диффузии, t - время. Согласно выводу Эйнштейна:
где µ - коэффициент трения диффундирующей частицы. Коэффициент трения макромолекулы µ M слагается аддитивно из коэффициентов трения звеньев цепи µ, поэтому
Последний результат дает возможность найти зависимость вязкости концентрированных растворов и расплавов полимеров от молекулярной массы, используя (2.63). Это важно сделать потому, что полученный результат легко проверить экспериментально. Необходимое для этого выражение для модуля упругости может быть легко получено, исходя из теории эластичности полимерных сеток, рассмотренной в разделе 2.2.4, согласно которой модуль упругости пропорционален плотности сшивки. Применим это положение к флуктуационной сетке зацеплений макромолекул, полагая, что число сшивок в единице объема обратно пропорционально ne и объему звена цепи l 3 где l -длина цепи. Тогда:
где М - молекулярная масса цепи. Опыт в целом подтверждает зависимость, однако в отдельных случаях наблюдается и несколько более сильная зависимость ŋ ~ М3,4. Поскольку многие физические свойства полимеров определяются их большим временем релаксации, целесообразно вернуться к соотношению (2.69). Оно может быть записано в следующем виде:
где Следует ожидать, что вязкоупругость какого-либо материала или жидкости будет проявляться в том случае, когда время воздействия на него t соизмеримо со временем релаксации Для полимерных жидкостей время релаксации
|

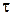 . Для того, чтобы теоретически рассчитать
. Для того, чтобы теоретически рассчитать 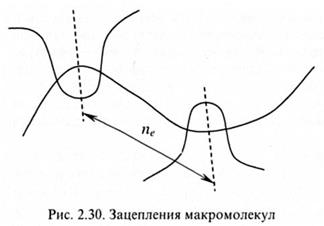
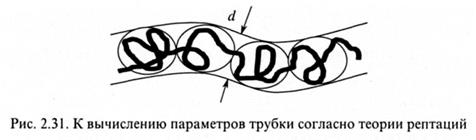
 > 104. Для столь длинных участков цепей справедливы все соображения, изложенные в разделе 2.1 о неизбежности сворачивания макромолекул в рыхлые клубки. Отрезок цепи между двумя зацеплениями образует так называемый субклубок или «блоб» с характерным размером
> 104. Для столь длинных участков цепей справедливы все соображения, изложенные в разделе 2.1 о неизбежности сворачивания макромолекул в рыхлые клубки. Отрезок цепи между двумя зацеплениями образует так называемый субклубок или «блоб» с характерным размером