Задача 4
§ 1. Прикордонний шар і його характерні товщини Відомо, що реальна рідина при обтіканні тіла через наявність в'язкості нібито прилипає до його поверхні. Тому швидкість потоку на поверхні тіла дорівнює нулю. При видаленні від тіла по нормалі до його поверхні швидкість буде збільшуватися. На деякій відстані від тіла вона буде близька до тієї, яка була б при обтіканні цього тіла ідеальною рідиною (рис. ХП.1). ідстань, на якому відбувається зміна швидкості від нуля (на стінці) до величини, що має місце в ідеальній рідині, характеризує область впливу в'язкості. Назвемо це відстань товщиною області впливу в'язкості. При зовнішньому обтіканні розглянута товщина, яку позначимо б, у міру віддалення від передньої критичної точки до задньої стінки буде рости. Введемо безрозмірну товщину впливу в'язкості, рівну значенню б, поділеній на характерний поздовжній розмір I обтічного тіла. Для крила таким розміром зазвичай є хорда.
Прандтль ще в 1904 р. відмітив, що величина
При великих числах Rе вплив в'язкості зосереджується в невеликій області біля тіла, тобто За аналогією з полем швидкостей можна розглядати поля температур і концентрацій речовин при наявності дифузії. Якщо температури тіла і потоку будуть різні, то величина області, в якій відбувається зміна від температури тіла до температури потоку, буде залежати від теплового числа Рейнольдса (Х.21). Позначивши товщину області і змінної температури Область, що безпосередньо прилягає до тіла, що обтікає, в котрій при великих R Якщо концентрація речовини на поверхні обтічного тіла відмінна від концентрації речовини в потоці протягом усього руху, то аналогічно тепловому прикордонному шару при великих значеннях дифузного числа Рейнольдса (Х.21) встановиться дифузний пограничний шар з товщиною При виникненні теплового та дифузійного прикордонних шарів за аналогією з динамічним з'являються тепловий та дифузійний слід і області постійних значень температур і концентрацій.
При обтіканні тіла можуть виникнути одночасно усі три прикордонні шари, товщини яких в загальному випадку різні. Далі буде показано умова однаковості цих товщин. Швидкості всередині прикордонного шару, як правило, монотонно збільшуються від нуля на стінці до значення на кордоні шару (рис. XII.2). Температура ж і концентрація в залежності від їх значень на стінці можуть або зростати всередині шару, або зменшуватись, як це показано на рис. XII.2. Так як практично величини швидкості, температури та концентрації до своїх значень на зовнішньому кордоні змінюються асимптотично (рис. XI 1.2), то при експерименті товщина шару визначається умовно. Зазвичай за товщину шару приймають таке значення координати Y, при якому швидкість, температура або концентрація в точці відрізняються від відповідної величини поза шаром на 1-2% (наприклад, u = 0,98U). В механіці рідин і газів часто користуються більш строго визначенішою товщиною прикордонного шару. Розглянемо фізичний зміст деяких інших характерних товщин пограничного шару. З'ясуймо насамперед, як впливає в'язкість на кінематику потоку, тобто на положення ліній струму. Задача 4 Замкнутый резервуар разделен на две части плоской перегородкой, имеющей квадратное отверстие со стороной а=400 мм, закрытое крышкой. Давление над жидкостью Ж (керосин) в левой части резервуара определяется показателем манометра Рм = 0,07 МПа (абс); давление воздуха в правой части – показателем мановаккуумметра Рв = 0,02 МПа (абс). Определить величину и точку приложения результирующей силы давления на крышку. Расстояние от поверхности жидкости до крышки h=1300 мм. Указание: Эксцентриситет центра давления для результирующей силы:
Решение: Геометрический центр крышки находится от поверхности жидкости на расстоянии h + a/2. Давление керосина на этой глубине
Сила давления на плоскую вертикальную стенку равна произведению давления в геометрическом центре на площадь поверхности, поэтому величина результирующей силы давления:
Эксцентриситет центра давления для результирующей силы:
Точка приложения результирующей силы к крышке находится на высоте h+a/2+е=1,3+0,2+0,0017=1,5017 м.
|


 залежить від числа Re. При малих числах Rе вона може бути дуже великою, отже,
залежить від числа Re. При малих числах Rе вона може бути дуже великою, отже,  буде
буде  > 1.
> 1.
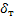 і ввівши безрозмірне
і ввівши безрозмірне 
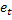 величина
величина  << 1.
<< 1.
 .
. .
. .
.



