Условия применимости уравнения Д.Бернулли
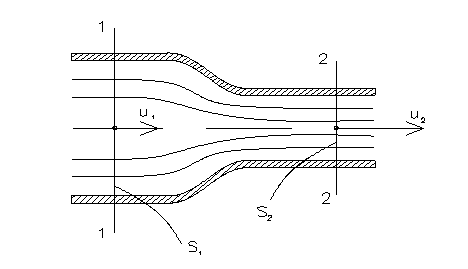
Распространим уравнение Бернулли на установившийся поток реальной жидкости. Для этого выберем на слабо деформированном участке потока живое сечение, вблизи которого движение можно считать плавноизменяющимся (например, сечение 1-1 на рис. II.05).
Рис. II.05
Через это сечение каждой элементарной струйкой за время dt вносится энергия, которая в соответсвии с вышеизложенным оказывается равной:
Учитывая, что
Найдем полную энергию, проносимую потоком жидкости через живое сечение 1-1. для этого необходимо, очевидно, просуммировать полученное выражение по всем струйкам данного живого сечения. Тогда получим:
Таким образом, полная энергия Е1 оказывается равной сумме двух интегралов, представляющих собой соответственно потенциальную и кинетическую энергию потока. Вычислим первый интеграл. Так как в сечении 1-1 величина
Но
Запишем второй интеграл в следующем виде:
Этот интеграл представляет собой, как уже указывалось, кинетическую энергию, проносимую потоком через сечение 1-1 за время
Это выражение по величине всегда меньше, чем действительная кинетическая энергия, вычисленная по действительным скоростям. обозначим отношение этих двух величин
Коэффициент Возвращаясь к поставленной задаче о вычислении второго интеграла в выражении (11.20), констатируем, что его значение можно выразить через среднюю скорость посредством введения коэффициента кинетической энергии
Подставив значения интегралов (11.21) и (11.23) в зависимость (11.20), получим:
Поделив выражения (11.24) и (11.25) на вес жидкости
Так как на участке потока между сечениями 1-1 и 2-2 часть энергии потока затрачивается на преодоление гидравлических сопротивлений и необратимо превращается в тепловую энергию,
Тогда:
или
Полученное уравнение и есть уравнение Д.Бернулли для установившегося потока реальной жидкости. По внешнему виду оно почти не отличается от полученного ранее уравнения Бернулли для элементарной струйки реальной жидкости. Тем не менее это уравнение обладает рядом отличительных особенностей, которые необходимо всегда помнить для правильного его использования. Во-первых, это уравнение записывается не для отдельных частиц жидкости, находящихся на одной и той же линии тока, а для различных сечений потока, при этом совершенно различно, какую частицу жидкости в сечении мы выбираем для определения величин Во-вторых, не обязательно, чтобы поток на всем протяжении между рассматриваемыми сечениями, для которых составляется уравнение Д.Бернулли, был близким к параллельноструйчатому. На этом участке он может претерпевать весьма резкие изменения своей формы. Совершенно необходимо лишь, чтобы в сечениях, для которых записывается уравнение Д.Бернулли, движение было плавно изменяющимся. Изменение формы (деформация) потока сопровождается затратами удельной его энергии и учитывается членом По аналогии с предыдущим будем называть величину Отметим, что при равномерном движении, когда
|

 .
. , и вынося за скобки все жидкости, прошедший через поперечное сечение элементарной струйки за время dt, равный
, и вынося за скобки все жидкости, прошедший через поперечное сечение элементарной струйки за время dt, равный  , перепишем это выражение в следующем виде:
, перепишем это выражение в следующем виде: .
.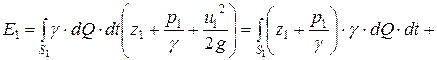
 (11.20)
(11.20) (см. зависимость 11.19), ее можно вынести за знак интеграла точно так же, как и
(см. зависимость 11.19), ее можно вынести за знак интеграла точно так же, как и  и
и  (постоянные величины).
(постоянные величины). .
.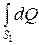 представляет собой расход потока Q. Поэтому:
представляет собой расход потока Q. Поэтому: . (II.21)
. (II.21)
 , то получим:
, то получим: .
. :
: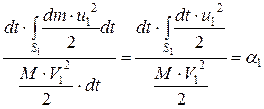 . (II.02)
. (II.02) (II.23)
(II.23) (II.24)
(II.24) (II.25)
(II.25) , получим значения полных удельных энергий потока в этих сечениях:
, получим значения полных удельных энергий потока в этих сечениях: ;
;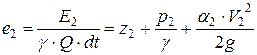 .
. . Очевидно также, что
. Очевидно также, что 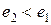 . Разница между этими удельными энергиями выразит потери удельной энергии потока на рассматриваемом участке движения:
. Разница между этими удельными энергиями выразит потери удельной энергии потока на рассматриваемом участке движения: .
.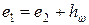 ,
, (II.26)
(II.26) и
и 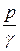 , так как при плавно изменяющемся движении
, так как при плавно изменяющемся движении  сохраняет постоянное значение для всех частиц жидкости в данном живом сечении. Необходимо лишь, чтобы значения
сохраняет постоянное значение для всех частиц жидкости в данном живом сечении. Необходимо лишь, чтобы значения  .
. - гидродинамическим напором потока, величину
- гидродинамическим напором потока, величину  - гидравлическим уклоном потока, а величину
- гидравлическим уклоном потока, а величину  - пьезометрическим уклоном потока.
- пьезометрическим уклоном потока.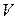 не изменяется по длине потока, то есть
не изменяется по длине потока, то есть  , гидравлический и пьезометрический уклоны совпадают:
, гидравлический и пьезометрический уклоны совпадают:
 . (II.27)
. (II.27)


