Уравнение Д.Бернулли для элементарной струйки реальной жидкости. Пьезометрический и гидравлический уклоны
При движении реальной жидкости между соседними струйками возникают силы трения, на преодоление которых затрачивается часть энергии жидкости. Поэтому удельная энергия жидкости в сечении элементарной струйки 2-2 будет мене удельной энергии жидкости в сечении 1-1 на некоторую величину
Следовательно, при установившемся движении реальной жидкости сумма четырех высот (геометрической, пьезометрической, скоростной и потерянной) или, что то же самое, сумма четырех удельных энергий 9положения, давления, кинетической и потерянной) не изменяется вдоль данной элементарной струйки. Легко изобразить уравнение Бернулли для рассматриваемого случая графически. Для этого следует, выбрав произвольную горизонтальную плоскость сравнения, отложить на ней в каждом сечении высоты
Рис. II.02
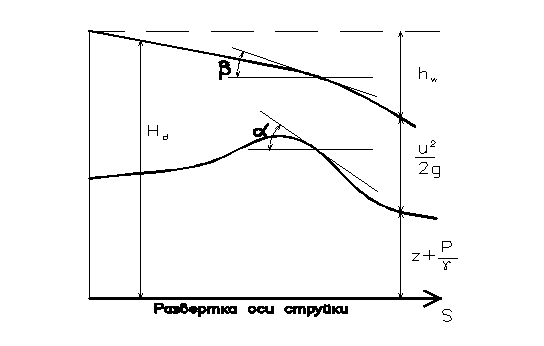
Проделаем теперь следующее построение: разверзнем криволинейную ось струйки s в горизонтальную прямую линию и в каждой ее точке отложим по вертикали значения удельных энергий
Соответственно падение гидравлической линии на единицу длины элементарной струйки назовем гидравлическим уклоном I:
На графике (рис. II.03) пьезометрический уклон представляется тангенсом угла наклона касательной к пьезометрической линии, а гидравлический уклон – тангенсом угла наклона касательной к гидравлической линии. Значение пьезометрического уклона может быть положительным или отрицательным в зависимости от того, увеличивается или уменьшается величина удельной потенциальной энергии
Рис. II.03
Гидравлиеческий уклон есть всегда величина положительная, так как полная удельная энергия движущейся части жидкости постепенно уменьшается по мере ее продвижения вдоль элементарной струйки, затрачиваясь на преодоление сил трения, превращаясь в тепловую энергию и рассеиваясь.
|

 , которую называют потерянной высотой или потерянной удельной энергией, затрачиваемой на преодоление гидравлических сопротивлений. Аналитически это положение запишется таким образом:
, которую называют потерянной высотой или потерянной удельной энергией, затрачиваемой на преодоление гидравлических сопротивлений. Аналитически это положение запишется таким образом: (11.14)
(11.14) ;
; 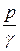 ;
;  и
и 
 и
и  , получим изображение пьезометрической и гидравлической линий. Падение пьезометрической линии на единицу длины элементарной струйки назовем пьезометрическим уклоном
, получим изображение пьезометрической и гидравлической линий. Падение пьезометрической линии на единицу длины элементарной струйки назовем пьезометрическим уклоном 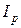 :
: . (11.15)
. (11.15)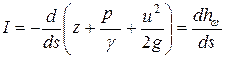 (11.16)
(11.16)