Математические модели ДСП
Процессы теплообмена в дуговой печи и прежде всего теплопереноса энергии, выделяемой в дуге, к поверхности ванны и футеровки имеют крайне важное значение для всего процесса плавки и вместе с тем носят очень сложный характер. Полную детерминированную модель процессов теплообмена дуговой печи, пригодную для использования в системах управления, создать весьма сложно и поэтому обычно используют упрощенные модели, которые идентифицируются по результатам экспериментов или промышленных плавок. Одна из таких моделей детерминированная, контролирующая модель, построена на основе использования мгновенных тепловых балансов ванны. В модели рассматриваются три составляющие мощности дуги: часть мощности, передаваемая путем теплопроводности и конвекции непосредственно в ванну Рд1, ее доля в общей мощности выражается через коэффициент
часть мощности, передаваемой от дуги к футеровке Рд2, доля этой составляющей равна
часть мощности, излучаемая дугой на всю поверхность ванны Рд3, доля этой составляющей равна
На основании анализа экспериментальных данных получены зависимости коэффициентов от силы тока дуги
где коэффициенты а, b, с, п различаются в зависимости от ступени напряжения трансформатора. Тепловой поток к ванне Qв определяется на основании балансового соотношения:
где Рассматривая эффективные тепловыепотоки излучения футеровки и ванны, как суммы всех отраженных тепловых потоков и соответственно собственных тепловых потоков излучения футеровки
где В, R, М, N, D – настроечные коэффициенты, определяемые при идентификации модели; Qф – тепловой поток потерь через отверстия в кладке, через футеровку и с охлаждающей водой. По уравнению (9) в любой момент времени при измеренных мощности дуги Рд, температуре футеровки Tф и ванны Тв можно рассчитать результирующий тепловой поток, воспринимаемый ванной Qв. Интегрируя Qв по времени, можно определить количество усваиваемого ванной тепла и по нему определить количество расплавившегося лома или изменение температуры жидкой ванны. Вторая контролирующая математическая модель, основанная на тепловом балансе ванны, предназначена для расчета степени расплавления шихты w (t)
где Еще одним примером математической модели тепловых процессов в ДСП может служить детерминированная контролирующая модель, построенная на основе мгновенных тепловых балансов печи. В полный мгновенный тепловой баланс дуговой печи входят следующие статьи. Приходная мощность (кВт): активная электрическая мощность Ра; тепловая мощность химических реакций, происходящих в сталеплавильной ванне и при окислении электродов, Qхим; тепловая мощность дополнительных источников энергии, например, природного газа, сжигаемого в газо-кислородных горелках Qт. Расходная мощность (кВт): тепловая мощность на расплавление и нагрев металла и шлака (полезная тепловая мощность) Qм; потери активной электрической мощности в трансформаторе и токоподводе Рэлп; тепловая мощность потерь теплоотдающей поверхностью кожуха печи Qп; тепловая мощность потерь с охлаждающей водой Qов; тепловая мощность потерь излучения через рабочее окно Qи; тепловая мощность потерь с отходящими газами Qог. Тепловая мощность, аккумулируемая футеровкой или отдаваемая ей в рабочее пространство Qакк, входит в расходную или приходную часть теплового баланса соответственно. Уравнение мгновенного баланса дуговой печи может быть записано следующим образом:
Из уравнения (11) может быть получено значение полезной тепловой мощности, усваиваемой металлом:
Активная мощность Ра определяется по показаниям электроизмерительных приборов. Мощность электрических потерь равна:
где Тепловая мощность химических реакций Qхим определяется по скорости окисления углерода, а в период кислородной продувки, когда она наиболее существенна, по расходу кислорода на продувку. Тепловая мощность топлива Qт определяется в период работы газокислородных горелок по расходу природного газа. Мощность аккумуляции Qакк может быть рассчитана предварительно в функции времени, отсчитываемого от начала плавки, или определена по измеренной скорости изменения температуры внутренней поверхности футеровки. Мощности тепловых потерь через футеровку Qп и излучением Qи принимаются постоянными по ходу плавки на основании специальных исследований или расчетов. Тепловая мощность потерь с охлаждающей водой Qов в определяется по расходу охлаждающей воды и по приращению ее температуры, измеряемой на входе и выходе (измерения могут производиться для всей печи или для отдельных водоохлаждаемых элементов). Тепловая мощность потерь с отходящими газами Qог определяется по их расходу, измеренному перед дымососом и температуре, измеренной на выходе из печи. Таким образом, по выражению (11) рассчитывается значение полезной тепловой мощности в данный момент времени по измеренным или рассчитанным составляющим баланса. Интегрируя Qм по времени, можно определить количество тепла, получаемого металлом за определенный отрезок времени, и пересчитать его на количество расплавившегося лома или изменение температуры металла. Уравнение теплового баланса можно использовать и для построения прогнозирующей математической модели температуры металла: например, для ДСП, перерабатывающей окатыши, загружаемые в жидкую ванну, прогноз температуры металла с момента расплавления проводится по системе уравнений.
где В АСУ ТП могут использоваться математические модели электропечного контура и физико-химических процессов плавки. Первые могут служить для расчета значений мощности, выделяемой в дуге по измеренным напряжению фазы Un и силе тока I, и заданий регулятором мощности. Вторые применяются для прогноза состава металла по ходу доводки, для определения длительности кислородной продувки и некоторых других технологических параметров. Их построение аналогично математическим моделям других сталеплавильных процессов.
|

 ; (4)
; (4) ; (5)
; (5)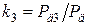 ; k3 = 1 – k1 – k2. (6)
; k3 = 1 – k1 – k2. (6) ;
; 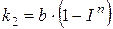 , (7)
, (7)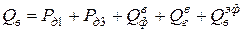 , (8)
, (8)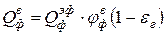 – тепловой поток от футеровки, воспринимаемый ванной;
– тепловой поток от футеровки, воспринимаемый ванной;  – эффективный тепловой поток излучения футеровки;
– эффективный тепловой поток излучения футеровки; 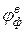 – угловой коэффициент излучения футеровки на ванну; eг – степень черноты печных газов;
– угловой коэффициент излучения футеровки на ванну; eг – степень черноты печных газов;  – тепловой поток от печных газов, воспринимаемый ванной;
– тепловой поток от печных газов, воспринимаемый ванной; 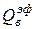 – эффективный тепловой поток излучения поверхности ванны;
– эффективный тепловой поток излучения поверхности ванны;  ; Fв и Fф – площади поверхности ванны и футеровки.
; Fв и Fф – площади поверхности ванны и футеровки. и ванны
и ванны  (Сф и Св – коэффициенты излучения футеровки и ванны; Тф и Тв – абсолютные температуры поверхности футеровки и ванны), можно получить уравнение:
(Сф и Св – коэффициенты излучения футеровки и ванны; Тф и Тв – абсолютные температуры поверхности футеровки и ванны), можно получить уравнение: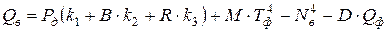 , (9)
, (9) , (10)
, (10) – усвоенное шихтой тепло;
– усвоенное шихтой тепло; 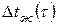 – температура перегрева жидкой фазы; ств, сж – удельная теплоемкость твердой шихты и жидкого металла; tпл – температура плавления шихты; q – скрытая теплота плавления лома; Мш – масса шихты;
– температура перегрева жидкой фазы; ств, сж – удельная теплоемкость твердой шихты и жидкого металла; tпл – температура плавления шихты; q – скрытая теплота плавления лома; Мш – масса шихты;  . (11)
. (11)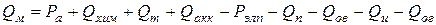 . (12)
. (12) . (13)
. (13)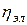 – электрический к.п.д., определяемый экспериментально и принимаемый постоянным.
– электрический к.п.д., определяемый экспериментально и принимаемый постоянным.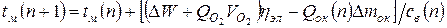 ; (14)
; (14)
 , (15)
, (15)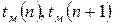 – температура металла в n -ый и n + 1-ый моменты времени, отстоящие друг от друга на 2…3 мин; DW – расход электроэнергии на интервале прогнозирования;
– температура металла в n -ый и n + 1-ый моменты времени, отстоящие друг от друга на 2…3 мин; DW – расход электроэнергии на интервале прогнозирования;  – тепловой эффект кислородной продувки;
– тепловой эффект кислородной продувки; 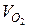 – количество кислорода, поданное в ванну, на интервале прогнозирования;
– количество кислорода, поданное в ванну, на интервале прогнозирования; 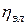 – энергетический к.п.д. печи на рассматриваемом интервале;
– энергетический к.п.д. печи на рассматриваемом интервале; 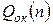 – расход тепла на плавление 1 т окатышей при температуре начала интервала прогнозирования;
– расход тепла на плавление 1 т окатышей при температуре начала интервала прогнозирования;  – масса окатышей, загруженных в течение интервала прогнозирования; св – приведенная теплоемкость ванны; см, сш, Сф – соответственно теплоемкости металла, шлака и футеровки;
– масса окатышей, загруженных в течение интервала прогнозирования; св – приведенная теплоемкость ванны; см, сш, Сф – соответственно теплоемкости металла, шлака и футеровки; 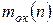 – масса окатышей, загруженных на начало интервала прогнозирования;
– масса окатышей, загруженных на начало интервала прогнозирования; 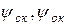 – средние значения угара скрапа и окатышей;
– средние значения угара скрапа и окатышей;  – содержание кремния в скрапе;
– содержание кремния в скрапе; 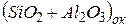 – содержание кремнезема и глинозема в окатышах; (FeO) – содержание FeO в шлаке; В – основность шлака; mф – масса футеровки, участвующей в теплообмене с жидкой ванной.
– содержание кремнезема и глинозема в окатышах; (FeO) – содержание FeO в шлаке; В – основность шлака; mф – масса футеровки, участвующей в теплообмене с жидкой ванной.


