Моменты распределения. Моменты распределения –обобщающая характеристика, определяющая характер распределения
Моменты распределения – обобщающая характеристика, определяющая характер распределения. Данное понятие взято из механики. Моментом
Моменты, в зависимости от величины · начальные; · начальные относительно · центральные. Начальные моменты рассчитывают, подставляя в предыдущую формулу:
В практике статистики применяют следующие начальные моменты:
· нулевого порядка:
· первого порядка:
· второго порядка:
· третьего порядка:
· четвертого порядка:
Условные моменты получают при
В практике статистики применяют следующие условные моменты:
· первого порядка:
· второго порядка:
· третьего порядка:
· четвертого порядка:
Центральные моменты получают, когда В практике статистики применяют следующие центральные моменты:
· нулевого порядка:
· первого порядка:
· второго порядка:
· третьего порядка:
· четвертого порядка:
На практике используются только центральные моменты третьего порядка для определения показателя асимметрии и четвертого порядка для определения показателя эксцесса.
|
-го порядка называется средняя из 
от некоторой величины:
– 
, (6.51)
;
: 
, (6.52)
, (6.53)
, (6.54)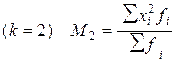
, (6.55)
, (6.56)
, (6.57)
, (6.58)
, (6.59)
, (6.60)
, (6.61)
, (6.62)
.
, (6.63)
, (6.64)
, (6.65)
, (6.66)
, (6.67)
