Основные свойства средней арифметической
1. Средняя арифметическая постоянной величины равна этой постоянной. 2. Если каждую варианту 3. Если каждую варианту 4. Сумма всех отклонений вариантов от средней (как простой, так и взвешенной) всегда равна нулю:
5. Сумма всех квадратов отклонений вариантов от средней (как простой так и взвешенной) всегда меньше суммы квадратов отклонений от любой другой произвольной величины:
6. Если все частоты разделить (умножить) на одно и то же постоянное число, средняя от этого не изменится. 7. Средняя многочлена равна многочлену средних:
Средняя гармоническая применяется при обобщении обратных Прямые значения признака Обратные значения признака Средняя гармоническая простая:
Средняя гармоническая взвешенная:
Средняя квадратическая простая:
Средняя квадратическая взвешенная:
Средняя кубическая простая:
Средняя квадратическая взвешенная:
Средняя геометрическая:
где
Мода – наиболее часто встречающееся значение признака в исследуемой совокупности. Медианой называется такое значение признака, которое стоит в середине ряда вариант расположенных по порядку возрастания или убывания (ранжированный ряд). Медиана делит ранжированный ряд пополам, в результате чего у половины единиц совокупности значение признака меньше медианы, а у половины больше медианы. Мода в дискретном вариационном ряду определяется частотой появления той или иной величины варианты, варианта с наибольшей частотой – мода. Мода в вариационном интервальном ряду рассчитывается по формуле:
где
Модальный интервал - это интервал, содержащий моду (имеющий наибольшую частоту). Медиана в дискретном вариационном ряду рассчитывается в зависимости от того, четное или нечетное количество элементов содержит ряд. При нечетном количестве единиц
При четном количестве единиц:
Медиана в интервальном вариационном ряду рассчитывается по формуле:
где
Медианный интервал это интервал, кумулятивная (накопленная) частота которого равна или превышает половину суммы частот. Квартиль делит ряд на четыре одинаковые части. Второй квартиль равен медиане. Расчет первого
Вместо медианного интервала при расчете
Вместо медианного интервала при расчете
|

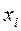 увеличить или уменьшить на одно и то же постоянное число, то новая средняя увеличится или уменьшится на это же число.
увеличить или уменьшить на одно и то же постоянное число, то новая средняя увеличится или уменьшится на это же число.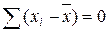 и
и  , (6.5)
, (6.5)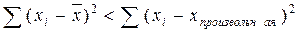 , (6.6)
, (6.6)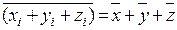 . (6.7)
. (6.7)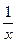 значениях изучаемого явления.
значениях изучаемого явления.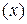 - такие значения, которые увеличиваются при увеличении определяющего показателя и характеризуемых ими явлений и уменьшаются при уменьшении.
- такие значения, которые увеличиваются при увеличении определяющего показателя и характеризуемых ими явлений и уменьшаются при уменьшении. - такие значения, которые увеличиваются при уменьшении определяющего показателя и характеризуемых ими явлений и уменьшаются при увеличении.
- такие значения, которые увеличиваются при уменьшении определяющего показателя и характеризуемых ими явлений и уменьшаются при увеличении.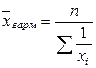 , (6.8)
, (6.8)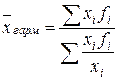 , (6.9)
, (6.9)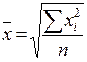 , (6.10)
, (6.10)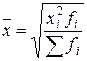 , (6.11)
, (6.11) , (6.12)
, (6.12)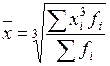 . (6.13)
. (6.13) ,
,  , (6.14)
, (6.14) – число значений признака;
– число значений признака; – знак перемножения;
– знак перемножения; – варианта признака.
– варианта признака.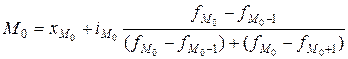 , (6.15)
, (6.15)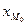 - минимальная граница модального интервала;
- минимальная граница модального интервала;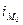 - величина модального интервала;
- величина модального интервала;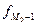 - частота интервала предшествующая модальному интервалу;
- частота интервала предшествующая модальному интервалу; - частота следующего за модальным интервалом;
- частота следующего за модальным интервалом;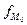 - частота модального интервала.
- частота модального интервала.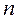 определяется номер варианты
определяется номер варианты 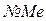 , которому соответствует медиана:
, которому соответствует медиана: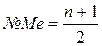 , (6.16)
, (6.16)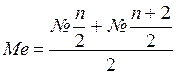 , (6.17)
, (6.17)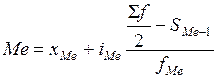 , (6.18)
, (6.18)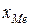 - начальное значение медианного интервала;
- начальное значение медианного интервала; - величина медианного интервала;
- величина медианного интервала; - сумма частот ряда;
- сумма частот ряда;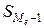 - сумма накопленных частот, всех интервалов, предшествующих медианному;
- сумма накопленных частот, всех интервалов, предшествующих медианному;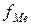 – частота медианного интервала.
– частота медианного интервала.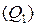 и третьего
и третьего 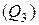 осуществляется по формулам:
осуществляется по формулам: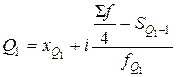 , (6.19)
, (6.19) берется интервал, в котором находится варианта, отсекающая ¼ численности частот:
берется интервал, в котором находится варианта, отсекающая ¼ численности частот: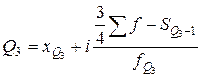 , (6.20)
, (6.20) берется интервал, в котором находится варианта, отсекающая ¾ численности частот.
берется интервал, в котором находится варианта, отсекающая ¾ численности частот.


