Корреляционно-регрессионный анализ
Корреляция (англ. Correlation – соответствие, соотношение) – взаимосвязь между признаками. Заключается в изменении средней величины результативного признака в зависимости от значения фактора (факторов). Регрессия – функция, позволяющая по величине одного корреляционно связанного признака вычислять средние значения другого. Корреляция, регрессия парная – корреляция, регрессия между двумя признаками: результативным Корреляция, регрессия множественная – взаимосвязь между несколькими признаками, один из которых является результативным признаком Корреляция линейная – корреляционная зависимость между признаками, носящая линейный характер. Корреляция криволинейная – корреляционная зависимость между признаками не носит линейный характер, а выражена соответствующей кривой – парабола, гипербола, экспонента, показательная функция и т.д. Для корректного применения корреляционного анализа требуется обоснование близости распределения значений факторного и результативного признаков к нормальному и формы связи к линейной. В противном случае необходимо использовать специальные приемы анализа или другие коэффициенты связи. Регрессия линейная – регрессионная функция, выраженная уравнением прямой. Линейное уравнение парной регрессии имеет вид:
Решение уравнения регрессии заключается в расчете его параметров. Наибольшее распространение из методов расчета параметров уравнения получил метод наименьших квадратов (МНК). МНК позволяет получать такие значения
При расчете параметров уравнения при помощи МНК необходимо решить систему из двух нормальных уравнений.
Также используют и готовые уравнения. Для расчета параметра
Для расчета параметра
так как
где Параметр Параметр Геометрически это тангенс угла наклона прямой регрессии Регрессия криволинейная – регрессионная функция выражена соответствующей нелинейной функцией – парабола, гипербола, экспонента, показательная, степенная функции и т.д. Расчет степенной функции:
проводят путем логарифмирования обеих частей уравнения:
Обозначив через
Метод наименьших квадратов (МНК) для оценки параметров функции регрессии по линеаризованной степенной функции дает следующую систему уравнений:
Рассчитав параметры Также можно использовать уравнения:
При определении вида функции в парной регрессии используют следующие методы: 1) графический, с использованием графика «корреляционное поле»; 2) аналитический, исходя из представления о материальной природе связи между изучаемыми признаками; 3) экспериментальный, со сравнением рассчитанных разных моделей между собой по различным критериям. Коэффициент парной корреляции показывает тесноту связи между двумя признаками. Парный линейный коэффициент корреляции
где
Коэффициент парной линейной корреляции показывает тесноту линейной связи между явлениями. Может принимать значения от -1 до 1. В статистике говорят, что если значения коэффициента парной корреляции · меньше 0,3 (-0,3) - связь положительная (отрицательная) слабая; · от 0,3 до 0,7 (от -0,3 до -0,7) - связь положительная (отрицательная) средняя; · свыше 0,7 (-0,7) - связь положительная (отрицательная) сильная; · равны 1 (-1) - связь функциональная положительная (отрицательная); · равны 0 – связь отсутствует. Коэффициент парной детерминации показывает часть вариации результативного признака, которая сложилась под влиянием включенного в парную модель фактора. Коэффициент парной детерминации
где
Коэффициент парной детерминации позволяет определять тесноту связи не только в линейных, но и в нелинейных моделях. Линейное уравнение множественной регрессии имеет вид:
Степенное [1] уравнение множественной регрессии имеет вид:
где
Параметры уравнения
Свободный член уравнения регрессии Коэффициенты регрессии Средний коэффициент эластичности
Средний b-коэффициент показывает, на сколько стандартных отклонений изменится вариация результативного признака, если у соответствующего данному b -коэффициенту фактора вариация увеличится на одно стандартное отклонение, при фиксированном положении остальных факторов. Рассчитывается как:
Множественный коэффициент корреляции
где Множественный коэффициент детерминации
где m - число параметров при переменных x; x - число наблюдений.
|

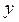 и факторным
и факторным 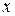 .
. , другие факторными признаками
, другие факторными признаками  .
. , (10.1)
, (10.1) , которые минимизируют сумму квадратов отклонений фактических значений
, которые минимизируют сумму квадратов отклонений фактических значений 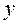 от теоретических
от теоретических  .
. , (10.2)
, (10.2) , (10.3)
, (10.3)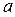 :
: , (10.4)
, (10.4) :
: , (10.5)
, (10.5) получим:
получим: или
или  , (10.6)
, (10.6)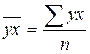 ;
;  .
. - это теоретическое значение результативного признака
- это теоретическое значение результативного признака 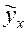 при
при  и только в этом случае имеет экономический смысл, если
и только в этом случае имеет экономический смысл, если  , параметр
, параметр  с осью ординат.
с осью ординат. называется коэффициентом регрессии. Коэффициент регрессии показывает, на сколько единиц, в среднем изменится результативный признак, если факторный признак увеличится на одну единицу.
называется коэффициентом регрессии. Коэффициент регрессии показывает, на сколько единиц, в среднем изменится результативный признак, если факторный признак увеличится на одну единицу.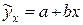 .
. , (10.7)
, (10.7)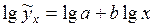 , (10.8)
, (10.8) , получим линейное уравнение регрессии:
, получим линейное уравнение регрессии: , (10.9)
, (10.9) ., (10.10)
., (10.10)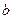 ,
, 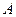 и составив линейное уравнение регрессии необходимо провести его потенцирование, чтобы вернуться к степенной функции.
и составив линейное уравнение регрессии необходимо провести его потенцирование, чтобы вернуться к степенной функции.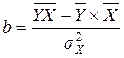 и
и  , (10.11)
, (10.11) рассчитывается как:
рассчитывается как: , (10.12)
, (10.12)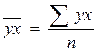 - среднее произведение результативного и факторного признаков;
- среднее произведение результативного и факторного признаков; - стандартное отклонение результативного и факторного признаков.
- стандартное отклонение результативного и факторного признаков. рассчитывают возводя в квадрат коэффициент парной корреляции
рассчитывают возводя в квадрат коэффициент парной корреляции  или по формуле:
или по формуле: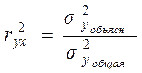 , (10.13)
, (10.13) – вариация признака y объясненная влиянием фактора
– вариация признака y объясненная влиянием фактора  ;
;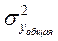 – общая вариация признака y.
– общая вариация признака y. , (10.14)
, (10.14) , (10.15)
, (10.15) - свободный член уравнения;
- свободный член уравнения; - коэффициенты регрессии, которые показывают, на сколько натуральных единиц изменится результативный признак, если соответствующий данному коэффициенту регрессии фактор увеличится на одну единицу, также в натуральном выражении при фиксированном положении остальных факторов.
- коэффициенты регрессии, которые показывают, на сколько натуральных единиц изменится результативный признак, если соответствующий данному коэффициенту регрессии фактор увеличится на одну единицу, также в натуральном выражении при фиксированном положении остальных факторов. множественной линейной регрессии находят при помощи метода наименьших квадратов (МНК). МНК дает систему нормальных уравнений:
множественной линейной регрессии находят при помощи метода наименьших квадратов (МНК). МНК дает систему нормальных уравнений: , (10.16)
, (10.16)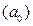 экономического смысла не имеет.
экономического смысла не имеет. показывают, на сколько единиц в среднем изменится результативный признак, при увеличении соответствующего фактора на одну единицу, при фиксированном положении остальных факторов.
показывают, на сколько единиц в среднем изменится результативный признак, при увеличении соответствующего фактора на одну единицу, при фиксированном положении остальных факторов. показывает, на сколько процентов изменится результативный признак, если соответствующий данному коэффициенту регрессии фактор увеличится на один процент, при фиксированном положении остальных факторов. Рассчитывается как:
показывает, на сколько процентов изменится результативный признак, если соответствующий данному коэффициенту регрессии фактор увеличится на один процент, при фиксированном положении остальных факторов. Рассчитывается как: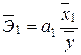 ;
;  ; …
; …  , (10.17)
, (10.17) ,
,  , …,
, …,  , (10.18)
, (10.18) показывает тесноту связи между результативным признаком и всеми включенными в модель факторами. Данный коэффициент может принимать значения от 0 до 1. Независимо от формы связи показатель множественной корреляции можно рассчитать как индекс множественной корреляции:
показывает тесноту связи между результативным признаком и всеми включенными в модель факторами. Данный коэффициент может принимать значения от 0 до 1. Независимо от формы связи показатель множественной корреляции можно рассчитать как индекс множественной корреляции: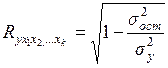 , (10.19)
, (10.19)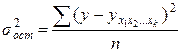 - остаточная дисперсия для уравнения
- остаточная дисперсия для уравнения  .
. показывает часть вариации результативного признака, которая сложилась под влиянием всех включенных в модель факторов. Формула скорректированного индекса множественной детерминации имеет вид:
показывает часть вариации результативного признака, которая сложилась под влиянием всех включенных в модель факторов. Формула скорректированного индекса множественной детерминации имеет вид: , (10.20)
, (10.20)


