Отбор факторов при построении множественной регрессии
1. Факторы должны быть количественно соизмеримы. Качественные показатели переводят в количественную форму, например, выражая их в баллах. 2. Факторы, включаемые в модель множественной регрессии, не должны быть: · интеркоррелированны – теснота связи между какими-то факторами больше, чем теснота связи между данными факторами и результативным признаком (например, · коллинеарные – считается, что две переменные коллинеарные (находятся в линейной зависимости), если Значимость уравнения регрессии оценивается при помощи критерия Фишера (F-критерия). В данном случае, при существенности уравнения регрессии, критерий Фишера фактический (берется из результатов, полученных при компьютерном расчете или рассчитывается самостоятельно) должен быть больше теоретического F-критерия (берется из таблицы «Значение критерия Фишера-Снедекора»). Фактический F-критерий для уравнения парной регрессии в целом рассчитывается как:
Оценку существенности уравнения регрессии проводят, сравнивая полученное значение F-критерия ( Фактический F-критерий для уравнения множественной регрессии в целом рассчитывается как:
где n - число наблюдений;
Частный F-критерий для фактора
Если Значимость параметров уравнения Для парной линейной модели.
Полученные фактические значения критерия Стьюдента сравнивают с табличными значениями при определенном уровне значимости Значимость коэффициентов регрессии и корреляции множественной модели регрессии оценивается при помощи критерия Стьюдента ( Фактический
Фактический
Если фактическое значение
Пример 24. Имеются данные о величине средней урожайности зерновых ц./га. и затратах на минеральные удобрения руб./на 1га. пашни по хозяйствам района (табл. 38). Необходимо: 1. Рассчитать коэффициент парной линейной корреляции, парной линейной детерминации, сделать выводы по каждому коэффициенту. 2. Построить уравнение парной линейной регрессии, спрогнозировать · максимально возможную величину · минимальную · 3. Провести статистическую оценку: · уравнения регрессии; · параметров уравнения регрессии и коэффициент корреляции. Таблица 38
Решение. 1. Рассчитаем коэффициент парной линейной корреляции:
Коэффициент парной линейной корреляции показывает, что затраты на минеральное уравнение оказывают сильное влияние на величину урожайности зерновых. Коэффициент парной линейной детерминации рассчитывается как квадрат коэффициента парной линейной корреляции;
Показывает, что 59% всей вариации результативного признака обусловлено включенным в модель фактором. 2. Уравнение парной линейной регрессии имеет вид При расчете параметров уравнения при помощи МНК необходимо решить систему из двух нормальных уравнений.
Рассчитаем все возможные значения в таблицу 38 и подставим в систему;
Разделим первое уравнение на 25, а второе на 1666
Вычтем из второго уравнение первое
Отсюда
Подставим в первое уравнение систему
Получили уравнение парной линейной регрессии:
Параметр Подставляя в уравнение значение фактора Рассчитаем максимально возможную величину
Рассчитаем минимально возможную величину
Рассчитаем величину
3. Проведем статистическую оценку уравнения регрессии его параметров и коэффициента корреляции. Статистическую значимость уравнения регрессии определяют при помощи критерия Фишера ( Рассчитаем фактическое значения критерия Фишера:
Теоретическое значение берем таблицы 5%-го уровня распределения F (приложение 3) Так как Статистическую значимость параметра Для парной линейной модели фактическое значения
Табличное значение Так как, фактические значения критерия Стьюдента больше табличных коэффициент регрессии и корреляции следует признать статистически значимым.
Общие положения по выполнения контрольной работы Задание для контрольной работы согласовывается с преподавателем, ему же по выполнении она представляется для проверки. По результатам преподаватель выставляет оценку (зачет), или количество заработанных балов.
|

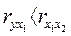 ).
).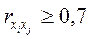 , и тем более мультиколлинеарные – более чем два фактора находятся в линейной зависимости.
, и тем более мультиколлинеарные – более чем два фактора находятся в линейной зависимости.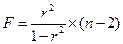 , (10.21)
, (10.21)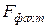 ) с табличным значением (
) с табличным значением (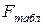 ), которое берут из таблиц критических значений F-отношений при определенном уровне значимости
), которое берут из таблиц критических значений F-отношений при определенном уровне значимости 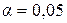 или
или 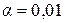 , и числе свободы:
, и числе свободы: 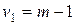 ,
, 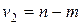 (таблицы Снедекора-Фишера – приложение 2).
(таблицы Снедекора-Фишера – приложение 2).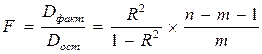 , (10.22)
, (10.22)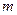 - число параметров при переменных x;
- число параметров при переменных x;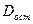 - остаточная сумма квадратов на одну степень свободы;
- остаточная сумма квадратов на одну степень свободы;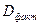 - факторная сумма квадратов на одну степень свободы;
- факторная сумма квадратов на одну степень свободы;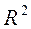 - коэффициент (индекс) множественной детерминации.
- коэффициент (индекс) множественной детерминации.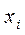 определяется как:
определяется как: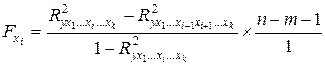 , (10.23)
, (10.23)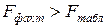 то уравнение регрессии значимо, если меньше незначимо.
то уравнение регрессии значимо, если меньше незначимо.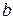 и коэффициента корреляции
и коэффициента корреляции 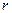 парной модели проверяют при помощи критерия Стьюдента –
парной модели проверяют при помощи критерия Стьюдента – 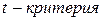 .
.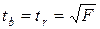 , (10.24)
, (10.24)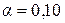 ,
, 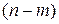 (приложение 1), где
(приложение 1), где  - число единиц наблюдения,
- число единиц наблюдения, 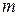 - число параметров уравнения регрессии.
- число параметров уравнения регрессии.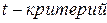 для коэффициента регрессии при i-м факторе рассчитывается как:
для коэффициента регрессии при i-м факторе рассчитывается как: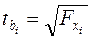 , (10.25)
, (10.25)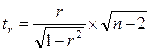 , (10.26)
, (10.26)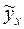 при различных значениях фактора, то есть рассчитать:
при различных значениях фактора, то есть рассчитать: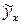 ;
;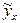 для средних значений фактора.
для средних значений фактора.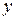
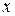
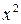
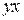
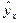
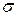
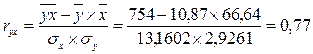 ,
,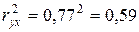
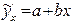
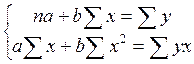
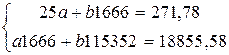
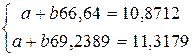
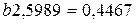
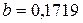
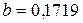 и рассчитаем
и рассчитаем 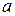 :
: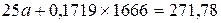
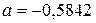
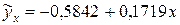
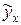 табл.38.
табл.38.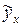 . Коэффициент регрессии
. Коэффициент регрессии 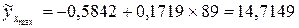
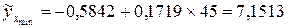
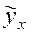 при средних значениях фактора
при средних значениях фактора 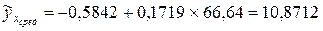
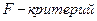 ).
).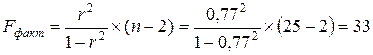
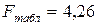 .
.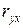 определяют при помощи критерия Стьюдента (
определяют при помощи критерия Стьюдента (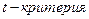 ).
).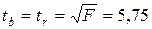
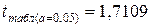 .
.


