Оцените с помощью F-критерия Фишера-Снедекора значимость уравнения линейной регрессии и показателя тесноты связи.
Оценку надежности уравнения регрессии в целом и показателя тесноты связи
Для проверки значимости уравнения выдвигаем две гипотезы: Н0: уравнение регрессии статистически не значимо; Н1: уравнение регрессии статистически значимо. По данным таблиц дисперсионного анализа, представленным на рисунке 3, Однако, если принять уровень значимости 10%, то можно говорить, что уравнение регрессии статистически значимо с вероятностью 90%. Также, судить о значимости уравнения регрессии и показателя тесноты связи, можно сравнивая Fфакт c Fкр(α, v1, v2). Значения множественного коэффициента корреляции R, нескорректированного (R-квадрат) и скорректированного (Нормированный R-квадрат) линейных множественных коэффициентов детерминации проведены на рисунке 3, в рамках регрессионной статистики. Множественный коэффициент корреляции R равен 0,715, что свидетельствует о тесной связи результативного показателя с факторными. Коэффициент множественной детерминации Скорректированный коэффициент множественной детерминации
|

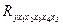 дает F-критерий Фишера:
дает F-критерий Фишера: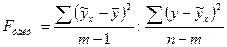 .
.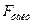 =2,937. Величина P – значение из этой же таблицы свидетельствует о том, что вероятность случайно получить такое значение F-критерия составляет 0,051, что превышает допустимый уровень значимости 5 %. Следовательно, полученное значение случайно, оно сформировалось под влиянием случайных факторов, т.е. не подтверждается статистическая значимость всего уравнения и показателя тесноты связи
=2,937. Величина P – значение из этой же таблицы свидетельствует о том, что вероятность случайно получить такое значение F-критерия составляет 0,051, что превышает допустимый уровень значимости 5 %. Следовательно, полученное значение случайно, оно сформировалось под влиянием случайных факторов, т.е. не подтверждается статистическая значимость всего уравнения и показателя тесноты связи 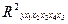 = 0,512 оценивает долю вариации результативного признака, обусловленную вариацией факторных признаков, здесь эта доля составляет 51,2% и указывает на хорошую степень обусловленности результата вариацией факторных признаков, т.е. на тесную связь между ними.
= 0,512 оценивает долю вариации результативного признака, обусловленную вариацией факторных признаков, здесь эта доля составляет 51,2% и указывает на хорошую степень обусловленности результата вариацией факторных признаков, т.е. на тесную связь между ними.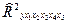 = 0,338 определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсией. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и потому может сравниваться по разным моделям с разным числом факторов.
= 0,338 определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсией. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и потому может сравниваться по разным моделям с разным числом факторов.


