Предложение 11.1 Пусть плоскость  задана уравнением
задана уравнением  и дана точка
и дана точка  . Тогда расстояние
. Тогда расстояние  от точки
от точки 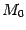 до плоскости
до плоскости  определяется по формуле
определяется по формуле

| (11.7)
|
Доказательство. Расстояние от точки 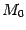 до плоскости
до плоскости  -- это, по определению, длина перпендикуляра
-- это, по определению, длина перпендикуляра  , опущенного из точки
, опущенного из точки 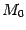 на плоскость
на плоскость  (рис. 11.9).
(рис. 11.9).

Рис.11.9.Расстояние от точки до плоскости
Вектор  и нормальный вектор n плоскости
и нормальный вектор n плоскости  параллельны, то есть угол
параллельны, то есть угол  между ними равен 0 или
между ними равен 0 или  , если вектор n имеет направление противоположное, указанному на рис. 11.9. Поэтому
, если вектор n имеет направление противоположное, указанному на рис. 11.9. Поэтому

Откуда

| (11.8)
|
Координаты точки  , которые нам неизвестны, обозначим
, которые нам неизвестны, обозначим  . Тогда
. Тогда  . Так как
. Так как 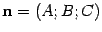 , то
, то  . Раскрыв скобки и перегруппировав слагаемые, получим
. Раскрыв скобки и перегруппировав слагаемые, получим

| (11.9)
|
Точка  лежит на плоскости
лежит на плоскости  , поэтому ее координаты удовлетворяют уравнению плоскости:
, поэтому ее координаты удовлетворяют уравнению плоскости: 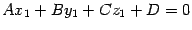 . Отсюда находим, что
. Отсюда находим, что  . Подставив полученный результат в формулу (11.9), получим
. Подставив полученный результат в формулу (11.9), получим  . Так как
. Так как 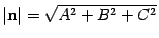 , то из формулы (11.8) следует формула (11.7).
, то из формулы (11.8) следует формула (11.7).