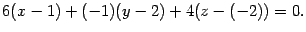Уравнение плоскости.
Пусть в трехмерном пространстве задана декартова прямоугольная система координат. Попробуем установить, какой вид может иметь уравнение плоскости. Для этого заметим, что все плоскости, перпендикулярные одной прямой, параллельны друг другу. Определение 11.2 Любая прямая, перпендикулярная плоскости, называется нормалью к плоскости, а любой ненулевой вектор на такой прямой мы будем называть нормальным вектором плоскости. Замечание 11.1 Из определения видно, что нормальный вектор у фиксированной плоскости определяется не однозначно. Все нормальные векторы одной плоскости коллинеарны друг другу и поэтому получаются один из другого умножением на число, отличное от нуля. Для того чтобы из параллельных плоскостей выбрать одну, достаточно задать точку, через которую проходит эта плоскость. Итак, если у плоскости известны нормальный вектор и точка, через которую она проходит, то плоскость определена однозначно. Теорема 11.1 Пусть вектор
является уравнением плоскости Доказательство. Пусть
Рис.11.1.
Вектор
Выразив скалярное произведение в левой части этого равенства через координаты сомножителей по формуле (10.1), получим формулу (11.1).
Пусть r -- радиус-вектор текущей точки
Такое уравнение обычно называют векторным уравнением плоскости Раскроем скобки в уравнении (11.1). Так как точка
Такое уравнение называется общим уравнением плоскости. Еще раз отметим, что в этом уравнении хотя бы один из коэффициентов Верно и обратное утверждение: Теорема 11.2 Всякое уравнение (11.3), в котором Доказательство. Условие
По теореме 11.1 такое уравнение является уравнением плоскости с нормальным вектором n, проходящей через точку
Теорема 11.1 позволяет написать уравнение плоскости, если известна точка этой плоскости и вектор, ортогональный плоскости. Однако, довольно часто встречаются задачи, где требуется получить уравнение плоскости, если известна точка, лежащая на ней, и два неколлинеарных вектора, лежащих или, что то же самое, параллельных плоскости. Покажем на примере, как решается такая задача. Пример 11.1 Требуется написать уравнение плоскости, проходящей через точку Решение. Векторное произведение
то есть
Раскрыв в этом уравнении скобки, приходим к окончательному ответу. Ответ:
|

 является нормальным вектором плоскости
является нормальным вектором плоскости  , проходящей через точку
, проходящей через точку  . Тогда уравнение
. Тогда уравнение
 -- некоторая точка плоскости
-- некоторая точка плоскости 
 лежит на плоскости
лежит на плоскости 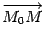 ортогонален вектору n. Если же взять точку
ортогонален вектору n. Если же взять точку  , не лежащую на плоскости
, не лежащую на плоскости  не будет ортогональным вектору n. Так как условием ортогональности двух векторов является равенство нулю их скалярного произведения (свойство 8, теорема 10.2), то условием того, что точка
не будет ортогональным вектору n. Так как условием ортогональности двух векторов является равенство нулю их скалярного произведения (свойство 8, теорема 10.2), то условием того, что точка  лежит в плоскости
лежит в плоскости 
 -- радиус-вектор точки
-- радиус-вектор точки 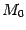 . Тогда уравнение (11.2) можно переписать в виде
. Тогда уравнение (11.2) можно переписать в виде
 является числом, которое обозначим буквой
является числом, которое обозначим буквой  . Тогда уравнение (11.1) принимает вид
. Тогда уравнение (11.1) принимает вид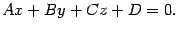
 отличен от нуля, так как
отличен от нуля, так как 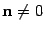 .
. , является уравнением плоскости, ортогональной вектору
, является уравнением плоскости, ортогональной вектору  .
. . Преобразуем уравнение (11.3) следующим образом:
. Преобразуем уравнение (11.3) следующим образом:
 .
. и параллельной векторам
и параллельной векторам 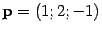 и
и  .
. по определению 10.26ортогонально векторам p и q. Следовательно, оно ортогонально искомой плоскости и вектор
по определению 10.26ортогонально векторам p и q. Следовательно, оно ортогонально искомой плоскости и вектор  можно взять в качестве ее нормального вектора. Найдем координаты вектора n:
можно взять в качестве ее нормального вектора. Найдем координаты вектора n:
 . Используя формулу (11.1), получим
. Используя формулу (11.1), получим