Декартовые координаты вектора в ПДСК на плоскости и в пространстве.
Мы рассмотрим сразу общий случай координатного пространства.Координатная плоскость будет частным случаем, хотя можно все рассуждения повторить (практически дословно) и для плоскости. Пусть М – произвольная точка координатного пространства Охуz. Определение. Вектор Введем обозначения:
Или, для произвольного вектора
Определение. Проекции вектора Теорема. (О координатах точки и ее радиус-вектора.) Координаты точки М в ПДСК в пространстве совпадают с декартовыми координатами её радиус-вектора. Доказательство.
рис.9. По определению, координаты
Теорема доказана. Заметим, что положение точки М в пространстве однозначно определяется ее координатами, т.е. существует взаимно однозначное соответствие между всеми точками пространства и упорядоченными тройками действительных чисел – их координатами. Вследствие этого, координатное пространство обозначают как декартов куб множества действительных чисел: Далее, очевидно, существует биекция и между всеми точкамипространства и их радиус-векторами, а значит и между радиус-векторами точек пространства и их декартовыми координатами как упорядоченными тройками действительных чисел:
В силу этого взаимно однозначного соответствия принято отождествлять радиус-вектор
Пусть
т.е. существует взаимно однозначное соответствие между всемивекторами пространства и всеми упорядоченными тройками действительных чисел, их декартовыми координатами. Отсюда сразу же вытекает следующая теорема. Теорема. (О равенстве векторов.) Два вектора равны тогда и только тогда, когда равны их декартовые координаты. Определение. Запись вектора в виде (2) или (3) называется егокоординатной формой записи. Теорема. (О действиях с векторами в координатной форме.) При сложении векторов их декартовые координаты складываются, а при умножении вектора на число каждая декартовая координата вектора умножается на это число. Иначе, пусть 2) Доказательство. Сразу же следует из свойств проекции вектора на ось:
Аналогично доказывается второе утверждение теоремы. Теорема доказана. Теорема. (О вычислении декартовых координат вектора.) Для того, чтобы вычислить декартовые координаты вектора нужно изкоординат его конца вычесть координаты его начала. Иначе, пусть
Доказательство. Пусть О(0; 0; 0) – начало координат. Тогда по правилу треугольника сложения векторов
рис.10.
Теорема доказана.
|

 называется радиус-вектором точки М.
называется радиус-вектором точки М. ,
,  ,
,  .
. :
: ,
,  ,
, 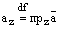 .
.
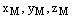 точки М есть координатыточек
точки М есть координатыточек  на координатных осях Ох, Оу, Оz соответственно, т.е.
на координатных осях Ох, Оу, Оz соответственно, т.е.  ,
,  ,
,  . Так как точки М и
. Так как точки М и  лежат в плоскости перпендикулярной оси Ох, то
лежат в плоскости перпендикулярной оси Ох, то  . По аналогичной причине
. По аналогичной причине  и
и  . Отсюда и следуют доказываемые равенства:
. Отсюда и следуют доказываемые равенства: ,
,  ,
, 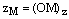 .
. . (Соответственно координатную плоскость как декартов квадрат множества действительных чисел:
. (Соответственно координатную плоскость как декартов квадрат множества действительных чисел:  )
) . (1)
. (1) с упорядоченной тройкой его декартовых координат:
с упорядоченной тройкой его декартовых координат: .
. . (2)
. (2) . Т.к. проекции вектора на оси не зависят от выбора точки его начала, то можно записать:
. Т.к. проекции вектора на оси не зависят от выбора точки его начала, то можно записать: , (3)
, (3) ,
,  ,
, 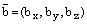 . Тогда: 1)
. Тогда: 1)  ;
; .
.
 .
.  .
. и
и  ,
,  – координаты его начала и конца. Тогда
– координаты его начала и конца. Тогда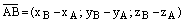 (4)
(4)
 . Векторы
. Векторы  и
и  являются радиус-векторами точек А и В соответственно и их декартовые координаты совпадают с координатами этих точек:
являются радиус-векторами точек А и В соответственно и их декартовые координаты совпадают с координатами этих точек:  ,
,  . Применяя теорему о действиях с векторами в координатной форме, получаем
. Применяя теорему о действиях с векторами в координатной форме, получаем .
.


