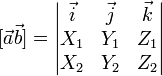Свойство векторного и смешенного произведения.
Геометрические свойства векторного произведения § Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения. § Модуль векторного произведения [ab] равняется площади S параллелограмма, построенного на приведённых к общему началу векторах a и b § Если e - орт векторного произведения a и b, а S - площадь параллелограмма, построенного на приведённых к общему началу векторах a и b, то для векторного произведения справедлива формула:
§ Если c - какой-нибудь вектор, π - любая плоскость, содержащая этот вектор, e - единичный вектор, лежащий в плоскости π и ортогональный к c, g - единичный вектор, ортогональный к плоскости π и направленный так, что тройка векторов ecg является правой, то для любого лежащего в плоскости π вектора a справедлива формула
Алгебраические свойства векторного произведения § § § § Выражение для векторного произведения в декартовых координатах Если два вектора a и b определены своими прямоугольными координатами
то иx векторное произведение имеет вид
Для запоминания этой формулы удобно использовать символ определителя:
|

 Править
Править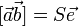

 (свойство антикоммутативности);
(свойство антикоммутативности); (свойство ассоциативности относительно умножения на скаляр);
(свойство ассоциативности относительно умножения на скаляр);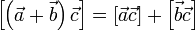 (свойство дистрибутивности по сложению);
(свойство дистрибутивности по сложению); для любого вектора a.
для любого вектора a.