Смешанное произведение векторов.
Определение. Смешанным произведением упорядоченной тройки векторов
Теорема. (Геометрический смысл смешанного произведения.) 1) Модуль смешанного произведения трех векторов численно равен объему параллелепипеда, построенного на трех данных векторах, как на его ребрах:
2) Доказательство. 1) Обозначим через
рис.3. Объем параллелепипеда V равен произведению площади основания S на высоту Н: Площадь основания S численно равна модулю векторногопроизведения:
Отсюда получаем:
2) Так как
Теорема доказана. Будем говорить, что тройки векторов Если же в тройке векторов меняются местами только два вектора, а один из векторов остается на своем месте, то такую перестановку мы будем называть не круговой перестановкой (или транспозицией). Так тройки Любую тройку векторов можно упорядочить 6-ю способами. Из них три тройки будут правыми и три тройки будут левыми. Если тройка Лемма. Круговая перестановка в тройке векторов не изменяет ее ориентации, а транспозиция векторов изменяет ориентацию тройки на противоположную. Доказательство проведите самостоятельно с использованием соответствующих картинок. 1) 2) 3) Доказательство. 1) По модулю все эти смешанные произведения равны друг другу, т.к. параллелепипед, построенный на данных трех векторах, как его ребрах, не зависит от того, в каком порядке мы записываем его ребра и, соответственно, не изменяется его объем. 2) Знак смешанного произведения упорядоченной тройки векторов зависит от ее ориентации, которая не меняется при круговой перестановке и меняется при транспозиции, откуда и следуют доказываемые равенства. 3) Воспользуемся уже доказанным равенством, определением смешанного произведения и свойством коммутативности скалярногопроизведения:
Следствие доказано.
|

 называется скалярное произведение первого вектора навекторное произведение второго вектора на третий и обозначается
называется скалярное произведение первого вектора навекторное произведение второго вектора на третий и обозначается .
. .
.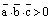 , если тройка
, если тройка  – правоориентированная и
– правоориентированная и  в противном случае.
в противном случае.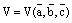 объем параллелепипеда, построенного на данных векторах, как на его ребрах.
объем параллелепипеда, построенного на данных векторах, как на его ребрах.
 .
. , а высота Н равна модулю проекции вектора
, а высота Н равна модулю проекции вектора  на вектор
на вектор  :
: .
. , ч.т.д.
, ч.т.д.
 , где
, где  , то знак смешанного произведениязависит от угла
, то знак смешанного произведениязависит от угла  . Если он острый, то смешанное произведение
. Если он острый, то смешанное произведение  , то кратчайший поворот первого вектора
, то кратчайший поворот первого вектора  осуществляется против часовой стрелки. В этом случае угол
осуществляется против часовой стрелки. В этом случае угол  и
и 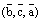 получились из тройки
получились из тройки  ,
,  ,
, 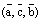 получаются из тройки
получаются из тройки  ;
; ;
; .
. .
.


