Векторное произведение векторов.Определение. Векторным произведением вектора 1) 2) тройка векторов 3)
рис.2. Обозначение: Из определения следует, что, если векторы 1) вектор 2) кратчайший поворот вектора 3) длина вектора Теорема. (Свойства векторного произведения.) 1). Антикоммутативность:
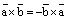2). Условие коллинеарности векторов:
3). Модуль векторного произведения численно равен площади параллелограмма, построенного на векторах Доказательство. 1) Пусть Действительно, т.к. И, наконец, 2) Если один из векторов или оба равны нулю, то они коллинеарные и их векторное произведение равно нулевому вектору, тут все очевидно. Пусть векторы 3) Следует из формулы площади параллелограмма. Теорема доказана.
|
на вектор 
называется третий вектор 
, который удовлетворяет следующим трем условиям:
и 
;
является правоориентированной;
.
.
, 
.
.
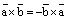. Рассмотрим вектор 
. Этот вектор удовлетворяет всем трем условиям определения векторногопроизведения вектора 
и 
. Далее, тройка векторов 
является правоориентированной, т.е. кратчайший поворот от вектора 
, ч.т.д.
или 
, а это в свою очередь равносильно тому, что 
, ч.т.д.
