Замечания 1.10.
1. Для доказательства формулы (1.9) можно использовать следующее соображение. Множество векторов на плоскости со стандартным базисом
2. Скалярное произведение можно записать в матричном виде: если
Для векторов на плоскости соответственно получаем
3. Координаты вектора
В самом деле, подставляя в (1.10) координаты
4. Формулы (1.9) и (1.10) совместно с геометрическими свойствами скалярного произведения имеют многочисленные приложения (см. разд. 1.6.2).
Пример 1.15. Даны векторы.
Найти скалярные произведения.
Решение. По формуле (1.10) вычисляем
Сравнивая вектор
Для нахождения скалярного произведения можно использовать матричную запись (см. пункт 2 замечаний 1.10). Например, векторам
Поэтому
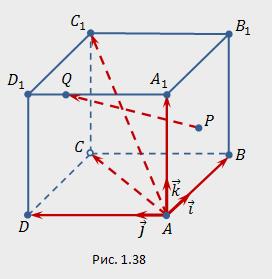
Пример 1.16. Прямоугольный параллелепипед
а) величину
б) длину ортогональной проекции вектора
Решение. Находим координаты векторов в стандартном базисе
(см. решение примера 1.12)
По формуле (1.10) находим скалярные произведения:
Длина
Теперь по геометрическому свойству 2 находим косинус искомого угла
т.е.
Алгебраическое значение длины ортогональной проекции находим по геометрическомусвойству 3:
|

 можно рассматривать как множество таких векторов в пространстве с базисом
можно рассматривать как множество таких векторов в пространстве с базисом  , у которых аппликата равна нулю. Поэтому формулу вычисления скалярного произведения векторов
, у которых аппликата равна нулю. Поэтому формулу вычисления скалярного произведения векторов  и
и  можно получить из (1.10), полагая
можно получить из (1.10), полагая  .
. и
и  координатные столбцы векторов
координатные столбцы векторов 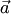 и
и  в стандартном базисе, то их скалярное произведение находится формуле:
в стандартном базисе, то их скалярное произведение находится формуле: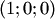 базисного вектора
базисного вектора  , приходим к первому равенству (остальные равенства получаются аналогично).
, приходим к первому равенству (остальные равенства получаются аналогично). со скалярными произведениями обнаруживаем, что при умножении вектора на базисный вектор получается соответствующая координата данного вектора. Этот результат иллюстрирует пункт 3 замечаний 1.10.
со скалярными произведениями обнаруживаем, что при умножении вектора на базисный вектор получается соответствующая координата данного вектора. Этот результат иллюстрирует пункт 3 замечаний 1.10. соответствуют координатные столбцы
соответствуют координатные столбцы построен на векторах (см. рис. 1.38). Точка
построен на векторах (см. рис. 1.38). Точка  — центр грани
— центр грани  , точка
, точка  делит ребро
делит ребро  в отношении
в отношении  . Требуется найти:
. Требуется найти: угла между векторами
угла между векторами 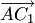 и
и  ;
; .
.
 была найдена в примере 1.12.
была найдена в примере 1.12.



