Скалярное произведение векторов. Рассмотрим два произвольных вектора: и
Рассмотрим два произвольных вектора:
Ненулевой вектор называется направляющим вектором прямой a, если он лежит либо на прямой a, либо на прямой, параллельной a.
Углом между ненулевыми векторами называется угол между прямыми, для которых данные вектора являются направляющими. Угол между любым вектором и нулевым вектором по определению считаем равным нулю. Если угол между векторами равен 90°, то такие вектора называются перпендикулярными. Угол между векторами будем обозначать так:
Скалярным произведением векторов
Совершенно аналогично, как в планиметрии, доказываются следующие утверждения: · Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны. · Скалярный квадрат вектора, то есть скалярное произведение его самого на себя, равно квадрату его длины. · Скалярное произведение двух векторов Перечислим основные свойства скалярного произведения, которые также доказываются аналогично планиметрическим. Для любых векторов 1. 2. 3. 4. Условие ортогональности двух векторов:
Т.о., для того чтобы два вектора были перпендикулярны необходимо и достаточно, чтобы сумма произведений соответствующих координат этих векторов была равна нулю.
|
и 
Определение 9.15.
и 
называется произведение их длин на косинус угла между ними:
заданных своими координатами, может быть вычислено по формуле 
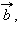и 
и любого числа λ справедливы равенства:
причем 
(переместительный закон).
(распределительный закон).
(сочетательный закон).
или 
.
